Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.8 - Ex. 35

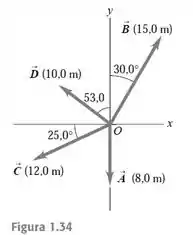
Determine os componentes x e y dos vetores A → ,   B → ,   C →   e   D → indicados na Figura 1.34.

Passo 1

Fala aí! tudo certinho? 😎

Nesse problema temos que determinar as componentes dos vetores dados na imagem do problema.

Parece complicado? 🤔

Temos que tomar muito cuidado com o ângulo.

Para cada vetor, V → vamos usar: V x = V cos ⁡ θ V y = V   s e n   θ

Os sinais das componentes correspondem ao quadrante em que o vetor se encontra.

Veja só! 😊

Passo 2

Vamos calcular o vetor A → . Para isso precisamos de duas componentes:

D a d o s :   A → = - 8 m θ A = - 90 °  

Portanto.

A x = 0

E

A y = 8 ⋅ sin ⁡ - 9 0

A y = - 8 m

As componentes de A → são negativas, pois estão para baixo.

Tranquilo até aqui? 😁

Passo 3

Vamos calcular o vetor B → . Para isso precisamos de duas componentes:

D a d o s :   B → = 15 θ B = 30 °   c o m   o   e i x o   y   o u   90 ° - 30 °   c o m   o   e i x o   x

B x = B ⋅ c o s   90 - 30

B x = 15 ⋅ 1 2 = 7,5 m

B y = B ⋅ sin ⁡ 90 - 30

B y = 15 ⋅ 3 2 = 13 m

As componentes de B → são positivas, pois estão para cima e para direita.

Bacana, não é? 😬

Passo 4

Agora vamos calcular o vetor C → :

D a d o s :   C → = - 12 θ C = 25 °   c o m   o   e i x o   x

C x = - C ⋅ cos ⁡ 25

C x = - 12 ⋅ 0,9063 = - 10,9 m

C y = - C ⋅ s e n   25

C y = - 12 ⋅ 0,4226 = - 5,07 m

As componentes de C → são negativas, pois estão para baixo e para esquerda.

Está acompanhando? 👀

Passo 5

Calculando o vetor D → :

D a d o s :   D → = 10 θ D = 53 °   c o m   o   e i x o   y   o u   90 ° + 53 °   c o m   o   e i x o   x

D x = D ⋅ cos ⁡ 90 - 53

D x = 10 ⋅ - 0,799 = - 7,99 m

D y = - 10 ⋅ sin ⁡ 90 + 53

D y = 10 ⋅ 0 , 602 = 6,02 m

As componentes de D → são negativas no eixo x, pois estão para a esquerda, e positivas no eixo y, pois estão para cima.

E aí! o que achou? Responde Aí! 😎

Resposta

A x = 0

A y = - 8 m

B x = 7,5 m

B y = 13 m

C x = - 10,9 m

C y = - 5,07 m

D x = - 7,99 m

D y = 6,02 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ao seguir um mapa do tesouro, você parte de um velho carvalho. Primeiro, caminha 825m diretamente para o sul, depois vira e segue 1,25k m a 30 ° do oeste para o norte e, finalmente, caminha 1,0k m a 4
Um empregado do serviço postal dirige um caminhão de entrega e faz o trajeto indicado na Figura 1.33. Use o método dos componentes para determinar o módulo, a direção e o sentido do deslocamento resul
Use um diagrama em escala para determinar os componentes x e y dos vetores seguintes. Para cada vetor, os números indicam o módulo do vetor e o ângulo que ele faz com o eixo + O x medido supondo-se um
O vetor A possui componentes A x = 1,30c m , A y = 2,25c m ; o vetor B possui componentes B x = 4,10c m , B y = – 3,75c m . Ache a) os componentes da soma vetorial A → + B → ; b) o módulo e a direção
O vetor possui comprimento igual a 2,80c m e está no primeiro quadrante a 60,0 ° acima do eixo O x . O vetor possui comprimento igual a 1,90c m e está no quarto quadrante a 60,0 ° abaixo do eixo O x (