Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 101

Determine a magnitude do campo gravitacional a uma distância r de uma barra fina e homogênea de comprimento infinito, cuja massa por unidade de comprimento é λ .

Passo 1

Primeiramente, vamos considerar um pedaço bem pequeno da barra com comprimento d l . Considerando a densidade linear do barra λ :

d m = λ d x

Agora vamos equacionar o campo gravitacional. Se liga nessa ilustração aqui embaixo:

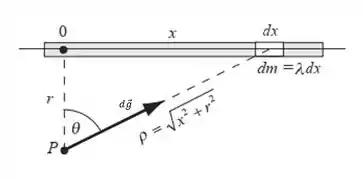
Para acharmos a distância entre nosso pedaço de anel e o eixo, podemos fazer um Pitágoras:

ρ 2 = x 2 + r 2

Passo 2

Nosso campo vai ficar assim:

d g = G d m x 2 + r 2

Como d m = λ d x :

d g = G λ d x x 2 + r 2

Repare que quando decompormos nosso vetor d g → no eixo horizontal eles irám se anular, pois temos uma distribuição simétrica. Para tentar entender isso um pouco melhor, veja que para cada pedacinho que temos na parte de esquerda, temos um na parte de diretita para anular seu efeito. Então nos resta apenas a componente horizontal:

d g x = G λ d x x 2 + r 2 cos ⁡ θ

Vamos colocar o d x em função de d θ :

t g θ = x r

Derivando,

sec 2 ⁡ θ   d θ = 1 r d x → d x = r s e c 2 θ d θ

Logo,

d g x = G λ r s e c 2 θ d θ x 2 + r 2 cos ⁡ θ = G λ r x 2 + r 2 cos ⁡ θ s e c 2 θ d θ

Como r x 2 + r 2 = c o s 2 θ r :

d g x = G λ r ⋅ c o s 2 ( θ ) s e c 2 θ cos ⁡ θ d θ

Portanto,

d g x = G λ r cos ⁡ θ d θ

Passo 3

Agora vamos integrar de - π 2 até π 2 , pois assim conseguimos pegar toda a barra

g x = ∫ π 2 π 2 G λ r cos ⁡ θ d θ = G λ r   ⋅ ∫ - π 2 π 2 cos ⁡ θ d θ

I = ∫ - π 2 π 2 c o s ⁡ ( θ ) d θ = 2 ⋅ ∫ 0 π 2 cos ⁡ θ d θ = 2 ⋅ 1 - 0 = 2  

Logo,

I = 2

Portanto,

g = 2 G λ r

Resposta

g = 2 G λ r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 13-39, uma partícula de massa m 1 = 0,67 k g está a uma distância de 23 cm de uma das extremidades de uma barra homogênea de comprimento L = 3,0 m e massa M = 5,0 k g . Qual é o módulo da forç
Um furo é feito da superfície da Terra até o seu centro, como na figura 11-30. Ignore a rotação da terra e a resistência do ar, e trate a Terra como uma esfera homogênea. (a) Qual é o trabalho necessá
Explique porque o campo gravitacional dentro de uma esfera maçica de massa homogênea é diretamente proporcional a r e não inversamente proporcional a r .
Uma barra uniforme deslgada possui comprimento L e massa M . Calcule o modulo da força gravitacional que a barra exerce sobre uma partícula de massa m situada ao longo do eixo da barra a uma distancia