Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 15
Explique porque o campo gravitacional dentro de uma esfera maçica de massa homogênea é diretamente proporcional a e não inversamente proporcional a .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos imaginar a esfera maciça abaixo:
Digamos que sua massa total é e a massa compreendida por é dada por .
Podemos relacionar essas duas massas através da sua densidade volumétrica. Temos que:
Portanto:
O campo gravitacional a uma distância é, assim:
Ou seja, a magnitude do campo é nula no centro e cresce linearmente com a distância dentro da esfera.
A figura abaixo nos mostra um gráfico do campo como uma função de para uma esfera maciça.
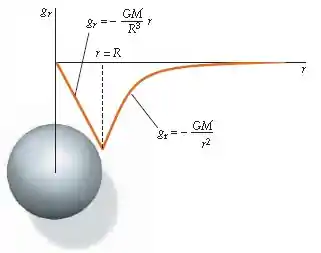
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A massa M está uniformemente distribuída ao longo de uma linha de comprimento igual a 2 L . Uma partícula de massa m está localizada a uma distância a acima do centro da linha sobre sua bissetriz orto
A massa M está uniformemente distribuída ao longo de um disco de raio a . Determine o módulo, a direção e o sentido da força gravitacional entre o disco e a partícula m localizada a uma distância x ac
Um fio uniforme de comprimento L e massa M está curvado em semicírculo. Calcule o módulo, direção e sentido da força gravitacional que o fio exerce sobre uma prticula de massa m situada no centro da c
Planetas não são uniformes por dentro. Normalmente eles são mais densos no nucelo e sua densidade vai descrevendo de dentro para fora té a superfície. Modele um planeta esfericamente simétrico, de mes
Um corpo com forma de anel fino possui raio a e massa M . Uma esfera uniforme de raio R e massa m é colocada com seu centro situado a uma distancia x à direita do centro do anel, sobre a linha que une