Uma esfera maciça e unifome de massa e raio está livre para girar em torno de um eixo horizontal que passa pelo seu centro. Um cortão está enrolado em torno da esfera e preso a um objeto de massa (figura 9-58). Suponha que o cordão não deslize na esfera. Determine (a) a aceleração do objeto e (b) a tensão no cordão.

Passo 1
a) Oláaa, querido! Cê tá bem?
Então, a gente tem um objeto preso a uma esfera por uma corda. A esfera está pressa pelo seu centro por um eixo. O peso desse objeto faz com que a esfera gire, ou seja, que ela tenha uma aceleração angular.
Ele pede a aceleração do objeto. Cara, como ele pede aceleração e temos várias forças envolvidas é uma boa a gente usar a segunda lei de Newton, ok?
E falou de usar a segunda lei de Newton, a gente pensa logo em fazer os diagramas de corpo livre da esfera e do objeto. Ficam assim:
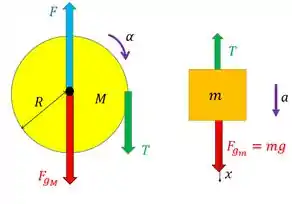
Percebe que está no sentido da aceleração. Bora lá usar a segunda lei de Newton!
Passo 2
Percebe que a tensão na esfera é a única força nela que não passa pelo seu centro, então ela é a única responsável por fazer a esfera girar, já que ela vai causar um torque na esfera.
E se a esfera está girando, a gente pode usar a segunda lei de Newton para rotação nela. Ela tem essa carinha:
A única força gerando o torque é a tensão . Ela é perpendicular ao raio da esfera, então o torque gerado vai ser , aí nossa lei de Newton fica:
E é o momento de inércia da esfera com relação a um eixo que passa pelo seu centro. Ele tem essa fórmulinha:
Substituindo:
Lembra como relacionamos aceleração angular e tangencial ? Assim oh:
Substituindo na nossa equação:
Mas a gente não sabe quem é e nem quem é , então precisamos de mais uma equação.
Passo 3
Bora fazer a segunda lei de Newton mais comum para o objeto:
Podemos substituir aqui a expressão para que achamos no passo anterior :
Agora é isolar :
Passo 4
b) Queremos a tensão agora. Temos que
Mas a gente acabou de achar , então podemos substituir aí:
Rearrumando