Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.3 - Ex. 13
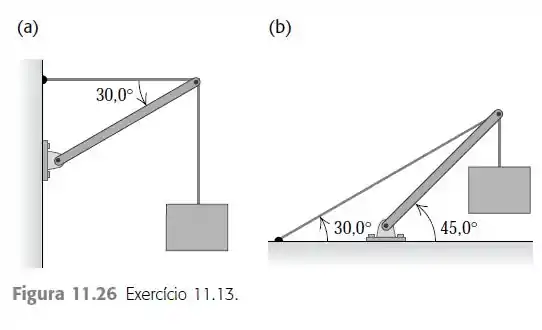
Determine a tensão em cada cabo e o módulo, a direção e o sentido da força exercida sobre a viga pelo pivô em cada um dos arranjos indicados na Figura 11.26. Em cada caso, seja o peso da caixa suspensa que está cheia de objetos de arte. A viga de suporte é uniforme e também possui peso . Comece cada caso com um diagrama do corpo livre para a viga.
Passo 1
Eaee, belezinha?? Bom... queremos determinar a tensão em cada cabo e o módulo, a direção e o sentido da força exercida sobre a viga pelo pivô em cada um dos arranjos indicados nas figuras abaixo:
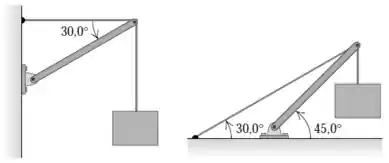
Para isso, temos os seguintes dados:
- Seja o peso da caixa suspensa que está cheia de objetos de arte;
- A viga de suporte é uniforme e também possui peso .
Dessa forma, devemos fazer o diagrama de corpo livre para cada sistema!! 😉
Passo 2
- Bom... vamos esboçar o diagrama de corpo livre para o suporte:
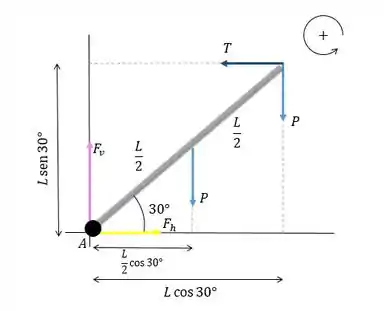
Vamos tomar a origem das coordenadas na dobradiça (ponto ) e para cima.
Seja e os componentes horizontais e verticais da força exercido no suporte pelo pivô.
A tensão no cabo vertical é o peso do objeto suspenso.
O peso do suporte pode ser utilizado para atuar no centro do suporte.
E seja o comprimento do suporte.
Passo 3
Então, aplicando a segunda lei de Newton na vertical, temos que:
Passo 4
Fazendo a soma dos torques sobre o ponto , temos que a força do pivô tem um braço de momento para este eixo e, portanto, não entra no torque da equação, assim:
E dessa forma, temos que:
Simplificando:
Isso implica que:
Passo 5
E então, aplicamos a segunda lei de Newton na horizontal:
Isso implica que:
Daí, sabemos que:
Passo 6
Agora que temos as componentes de , podemos calcular a sua magnitude e direção, da seguinte maneira:
Isso implica que:
E a direção é dada por:
Passo 7
Caso (b): Partindo para o próximo diagrama, temos:
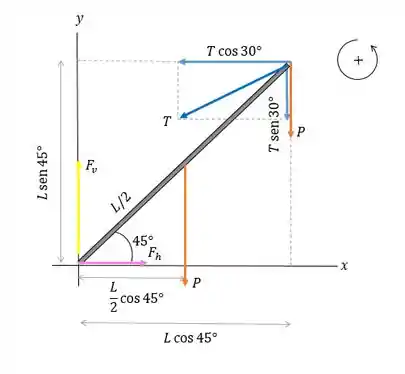
Observe que a tensão foi substituída por seus componentes e. O torque devido a é igual à soma dos torques de sua componentes, assim:
O comprimento se divide da equação. A equação também pode ser simplificada, observando que:
Então:
Isso implica que:
Passo 8
E então, aplicamos a segunda lei de Newton na horizontal:
Isso implica que:
Daí sabemos que:
Passo 9
E então, aplicando a segunda lei de Newton na vertical, temos que:
Passo 10
Agora que temos as componentes de , podemos calcular a sua magnitude e direção, da seguinte maneira:
Isso implica que:
E a direção é dada por:
Passo 11
Em cada caso, a força exercida pelo pivô não atua ao longo do suporte. Considere o torque total sobre a extremidade superior do suporte.
Se a força de pivô agisse ao longo do suporte, teria zero torque sobre esse ponto.
As duas forças que atuam nesse ponto também têm torque zero e haveria um torque diferente de zero, devido ao peso do suporte.
O torque total sobre esse ponto não seria então zero, violando a segunda condição de equilíbrio.
Resposta
Caso (a):
Caso (b):