Uma viga não uniforme com m de comprimento e pesando kN faz um ângulo de com a horizontal. Ela é mantida na horizontal com auxílio de um pivô sem atrito em sua extremidade direita superior e por um cabo ortogonal à viga situado a m abaixo da sua extremidade (Figura 11.31). O centro de gravidade da viga está a m ao longo da viga e do pivô. Um equipamento leve exerce uma força de kN de cima para baixo na extremidade inferior esquerda da viga. Calcule a tensão no cabo e os componentes horizontal e vertical da força exercida sobre a viga pelo pivô. Comece desenhando um diagrama do corpo livre para a viga.
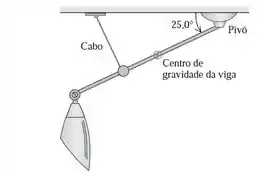
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente calcular a tensão no cabo e as componentes horizontal e vertical da força exercida sobre a viga pelo pivô. Pra isso, a gente sabe que a viga tem de comprimento, pesa e faz um ângulo de com a horizontal.
Além disso, nós sabemos que o cabo está m abaixo da sua extremidade, que o centro de gravidade da viga está a m ao longo da viga e do pivô e que um equipamento leve exerce uma força de kN de cima para baixo na extremidade inferior esquerda da viga.
Esboçando tudo isso em um diagrama de corpo livre (DCL), vamos ter:
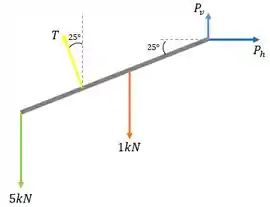
Então, vamos usar as equações de equilíbrio do torque e da força para encontrar a tensão e as componentes do pivô.
Vamos lá!
Passo 2
O cabo é dado como perpendicular ao feixe, de modo que a tensão é encontrada através de torques sobre o ponto de articulação. Assim, somando os torque a partir do ponto do pivô, vamos ter:
Calculando esses produtos e somando, temos:
Passo 3
Considere para cima e para a direita como positivos. Aplique a primeira condição para o equilíbrio translacional da Equação na viga na direção vertical:
Valeu, galera! Até a próxima! 😉
Resposta
Força horizontal:
Força vertical: