Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 6.1 - Ex. 44
Os vetores unitários e estão no plano xy. Eles formam os ângulos e , respectivamente, com o eixo +x. (a) Use trigonometria para encontrar diretamente as componentes x e y dos dois vetores. (Sua resposta deve ser em termos dos ângulos.) (b) Considerando o produto escalar de por , mostre que .
Passo 1
Letra (a)
Olá, querido! Como vai aí esse coração? Bora começar!
Ele quer que a gente ache as componentes de e . Ele diz que faz um ângulo com o sentido positivo de . E faz um ângulo com o sentido positivo de . E que esses vetores são unitários, ou seja, o módulo desses dois caras vale 1.
Vamos fazer um esquema dessa situação:
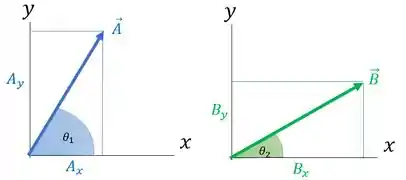
Vamos considerar que é maior que . A componente de em , que a gente vai chamar de , a gente pode obter usando uma relação da trigonometria:
Só que o módulo de é , porque é um vetor unitário. Então:
Para a gente achar a componente , fazemos um raciocínio análogo:
Já que :
Passo 2
Usando exatamente a mesma ideia, a gente tira que:
Como também é unitário, temos , logo:
E para :
Passo 3
Letra (b)
Como ele fala de produto escalar, vamos fazer o produto escalar . Temos que
Então o produto escalar fica:
Para calcular esse produto escalar a gente faz o produto entre as componentes de cada vetor e soma ao produto entre as componentes de cada vetor:
Passo 4
Agora a gente tem que lembrar que o produto escalar tem outra expressão:
Sendo que , pois são vetores unitários, e é o ângulo entre eles. Substituindo esses módulos ali na expressão:
Mas quem é vai ser ? Vamos fazer uma figura com os dois vetores juntos para achar :
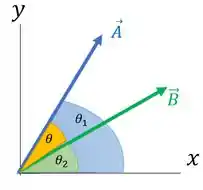
Da figura a gente vê que como a gente considerou que era maior podemos dizer que: . Então o produto escalar fica assim:
Obs: a gente até poderia ter considerado maior. Não faz diferença. Se fosse maior, teríamos que . Só que jogando isso no produto escalar, poderíamos fazer:
E como a função cosseno tem essa propriedade: , poderíamos dizer:
Que dá a mesma coisa que a gente achou quando fez ser maior!
Passo 5
Temos duas expressões para o produto escalar entre nossos vetores agora:
Igualando a equação 1 com a equação 2:
Resposta
Letra (a): ,,
Letra (b): ver solução