Um disco horizontal uniforme, de massa e raio, gira em torno do eixo vertical que passa pelo seu centro de massa com uma rapidez angular . Quando o disco, girando, é largado sobre uma mesa horizontal, forças de atrito cinético sobre o disco se opõem ao seu movimento de rotação. Seja o coeficiente de atrito cinético entre o disco e a mesa. (a) Determine o torque exercido pela força de atrito sobre um elemento circular de raio e largura . (b) Determine o torque total total exercido pelo atrito sobre o disco. (c) Determine o tempo que o disco leva para parar de girar.
Passo 1
- A força de atrito vai exercer torque no disco, fazendo com que ele rode. Esse torque pode ser calculado como:
- Integrando a expressão do de 0 a R vamos encontrar o trabalho total.
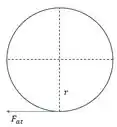
Mas , então:
A massa do disco é:
Mas é igual à massa por unidade de área, então
Passo 2
Passo 2
c) Falta só a gente encontrar o tempo:
Dividindo as duas para sumir a aceleração:
O momento de inércia para o disco é:
Substituindo o que já temos:
Resposta
a)
b)
c)