Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 18

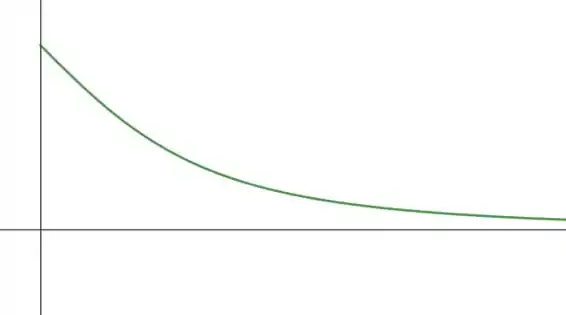
Um disco não condutor de raio a está no plano z = 0 com seu centro na origem. O disco está uniformemente carregado e tem uma carga total Q . Determine E z no eixo z em em (a) z = 0,2 a , (b) z = 0,5 a , (c) z = 0,7 a , (d) z = a e (e) z = 2 a . (f) Use seus resultados para fazer um gráfico de E z versus para valores positivos e negativos de z . (Considere que estas distâncias sejam exatas.)

Passo 1

Vamos usar a fórmula para o campo elétrico de um disco uniformemente carregado:

E z = σ 2 ε 0 1 - 1 1 + a 2 z 2 = Q 2 π ε 0 a 2 1 - 1 1 + a 2 z 2

  1. Fazendo z = 0,2 a , temos:

    2. E z = Q 2 π ε 0 a 2 1 - 1 1 + a 2 0,2 a 2 = 0,128 Q ε 0 a 2

  2. Fazendo z = 0,5 a , temos

    3. E z = Q 2 π ε 0 a 2 1 - 1 1 + a 2 0 , 5 a 2 = 0,088 Q ε 0 a 2

  3. Fazendo z = 0,7 a , temos

    4. E z = Q 2 π ε 0 a 2 1 - 1 1 + a 2 0 , 7 a 2 = 0,068 Q ε 0 a 2

  4. Fazendo z = a , temos

    5. E z = Q 2 π ε 0 a 2 1 - 1 1 + a 2 a 2 = 0,047 Q ε 0 a 2

  5. Fazendo z = 2 a , temos

    6. E z = Q 2 π ε 0 a 2 1 - 1 1 + a 2 2 a 2 = 0,017 Q ε 0 a 2

    Passo 2

  6. Veja o gráfico na figura abaixo:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco não-condutor de raio R está no plano z = 0 com seu centro na origem. O disco tem uma densidade σ . Determine o valor de z para o qual E z = σ / ( 4 ε 0 ) . Observe que, nesta distância, a int
Mostre que a intensidade do campo elétrico E no eixo de um anel carregado de raio a tem valor máximo em z = ± a / 2 . (b) Esboce a intensidade E do campo versus z para valores positivos e negativos de
Um anel com raio a está no plano z = 0 com seu centro na origem. O anel está uniformemente carregado e tem uma carga total Q . Determine E z no eixo z em (a) z = 0,2 a , (b) z = 0,5 a , (c) z = 0,7 a
Usando uma planilha eletrônica ou uma calculadora gráfica faça um gráfico da intensidade do campo elétrico no eixo de um disco que tem um raio a = 3,00c m e uma densidade superficial de carga σ = 0,50