Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.Problemas - Ex. 93

Um disco uniforme fino possui massa M e raio R. Fazemos um buraco circular de raio R/4 centralizado em um ponto situado a uma distância R/2 do centro do disco.

a) Calcule o momento de inércia do disco com o buraco em relação a um eixo perpendicular ao plano do disco passando pelo centro original do disco. (Sugestão: Ache o momento de inércia do disco que foi retirado do disco maciço.)

b) Calcule o momento de inércia do disco com o buraco em relação a um eixo perpendicular ao plano do disco passando pelo centro do buraco.

Passo 1

Oi, galerinha! Tudo bom?

O Momento de Inércia Final será o momento de inércia do disco sem o buraco menos o momento de inércia que o buraco tem, girando-o a parir do centro do disco principal, ou seja, de uma distância de R / 2 . O desenho é esse:

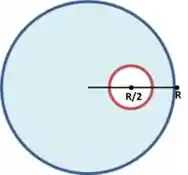
Com isso podemos inicialmente buscar calcular qual seria o momento deste buraco, tendo em vista que o momento de inércia do disco inteiro seria:

I = M R 2 2

Vejasó!

Passo 2

  1. Para calcular o momento de inércia do buraco, devemos utilizar o teorema dos eixos paralelos, que irá relacionar o momento de inércia de um disco de raio R / 4 girando em torno de uma distância R / 2 , ou seja

    2. I b = m 2 R 4 2 + m R 2 2 = 9 m R 2 32

    Show?

    Passo 3

    Entretanto ainda devemos calcular qual é a porção m em relação a M .

    Tomando que π R 2 = M , teremos que:

    m = π R / 4 2 = π R 2 16

    Com isso:

    m = M 16

    Tranquilo até aqui?

    Passo 4

    Logo, como o momento de inércia total será o momento do disco maciço menos o momento do buraco, o momento de inércia do disco com um buraco será então:

    I 1 = I d i s c o - I b

    I 1 = M R 2 2 - M 16 9 M R 2 32 = 247 M R 2 512

    Estamos quase lá!

    Passo 5

  2. Para calcular o novo momento de inércia, devemos tomar o momento de inércia do disco inteiro mais o M d 2 , proveniente do teorema dos eixos paralelos, e subtrair o momento de inércia do buraco, ou seja:

I = M R 2 2 + M R 2 2 - M 16 R 4 2 = 383 512 M R 2

E fim! O que achou? Responde Aí!

Resposta

  1.   I =     247 M R 2 512
  2. I = 383 512 M R 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento de inércia de massa do conjunto em relação ao eixo z . A densidade do material é 7,85M g / m 3 .
Determine o momento de inércia I z do tronco de cone com uma depressão cônica. O material tem densidade de 200k g / m 3 .
Determine o momento de inércia de massa da manivela em relação ao eixo x ' . O material é aço, com densidade ρ = 7,85M g / m 3 .
Cada um dos três elementos finos tem massa m . Determine o momento de inércia do conjunto em relação a um eixo perpendicular à página e que passa pelo ponto central O .
O pêndulo consiste em duas hastes finas A B e O C , que tem massa de 3k g / m . A placa fina tem massa de 12k g / m 2 . Determine a localização y - do centro de massa G do pêndulo; depois, determine o