Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.1 - Ex. 3

Um projetista de páginas da Internet cria uma animação na qual um ponto da tela do computador possui posição r → = [ 4,0 c m + ( 2,5 c m / s 2 ) t 2 ] i ^ + ( 5,0 c m / s ) t   j ^ a) Ache o módulo, a direção e o sentido da velocidade média do ponto para o intervalo entre t 1 = 0 e t 2 = 2,0 s . b) Ache o módulo, a direção e o sentido da velocidade instantânea para t 1 = 0 e t 2 = 2,0 s . c) Faça um desenho da trajetória do ponto no intervalo entre t 1 = 0 e t 2 = 2,0 s e mostre as velocidades calculadas em (b)

Passo 1

Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Aqui temos uma partícula que possui sua posição dada por uma equação dependente do tempo.

A partir dela, iremos encontrar a sua velocidade, para isso iremos utilizar a derivada.

Passo 2

  1. Temos que:

    2. r → = [ 4,0 c m + ( 2,5 c m / s 2 ) t 2 ] i ^ + ( 5,0 c m / s ) t   j ^

    E a partir deste podemos calcular x e y para qualquer t .

    Então, para t = 0 : r → = 4,0 c m

    E para t = 2 s : r → = ( 14 c m ) i ^ + ( 10 c m / s ) j ^

    Agora vamos calular o ∆ t , ∆ x e ∆ y :

    ∆ t = 2 s - 0 = 2 s

    ∆ x = 14 c m - 4 c m = 10 c m

    ∆ y = 10 c m - 0 - 10 c m

    Passo 3

    E então podemos calculara velocidade média de x e y :

    Em x :

    v m é d i a x = ∆ x ∆ t = 10 c m 2 s = 5 c m / s

    Em y :

    v m é d i a y = ∆ y ∆ t = 10 c m 2 s = 5 c m / s

    Dessa forma, o modulo da velocidade média pode ser calculado por:

    v = v m é d i a x 2 + v m é d i a y 2

    v = 5 m 2 + 5 c m 2 = 7,1 c m / s

    E para encontrar o modulo, fazemos:

    tan ⁡ α = v m é d i a y v m é d i a x

    tan ⁡ α = 5 c m 5 c m = 1

    α = tan - 1 ⁡ ( 1 ) = 45 °

    Passo 4

  2. Vamos derivar r → para que possamos encontrar a velocidade instantânea:

    3. v → = d r → d t = ( 5 c m / s 2 ⋅ t )   i ^ + ( 5 c m / s 2 )   j ^

    Para t = 0 : v x = 0 v y = 5 c m / s ⇒ v = 5 c m / s e α = 90 °

    Para t = 1 s : v x = 5 c m / s v y = 5 c m / s ⇒ v = 7,1 c m / s e α = 45 °

    Para t = 2 s : v x = 10 c m / s v y = 5 c m / s ⇒ v = 11 c m / s e α = 27 °

    Passo 5

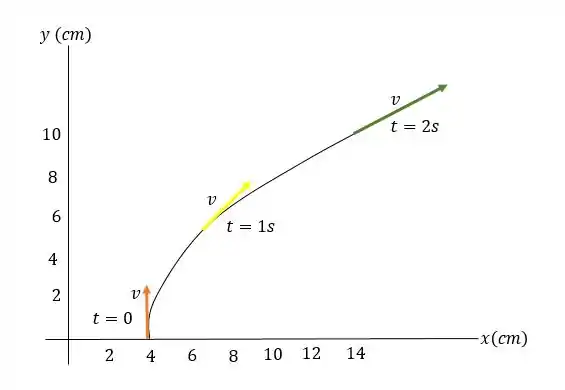
  3. A trajetória do gráfico de y x :

O esboço mostra que a velocidade instantânea em qualquer   t é tangente à trajetória.

Resposta

  1. v = 7,1 c m / s e direção 45 °
  2. Para t = 0 ⇒ v = 5 c m / s e α = 90 °

    3. Para t = 1 s ⇒ v = 7,1 c m / s e α = 45 °

    Para t = 2 s ⇒ v = 11 c m / s e α = 27 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um certo instante, um ciclista está 40,0m a leste do mastro de um parque, indo para o sul com uma velocidade de 10,0m / s . Após 30,0s , o ciclista está 40,0m ao norte do mastro, dirigindo-se para
O vetor posição de um íon é inicialmente r=5,0 i- 6,0j+ 2,0 k e 10s depois passa a ser r=- 2 i ,+ 8 j ,- 2 k , com todos os valores em metros. Na notação de vetores unitários, qual é a velocidade médi
A posição de um esquilo correndo em um parque é dada por 0,280m / s t +0,0360 m / s 2 t 2 i → + 0,0190m / s 3 t 3 j → . (a) Quais são v x ( t ) e v y ( t ) , os componentes x e y da velocidade do esqu
Na Fig. 33-77, um albatroz está planando horizontalmente com uma velocidade constante de 15m / s acima de um terreno plano, movendo-se em um plano vertical que inclui o Sol. A ave se aproxima de uma p
Um projetista de páginas da Internet cria uma animação na qual um ponto da tela do computador possui posição r → = [ 4,0 c m + ( 2,5 c m / s 2 ) t 2 ] i ^ + ( 5,0 c m / s ) tj ^ a) Ache o módulo, a di