Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 15.Exercício - Ex. 34

A distância entre dois ventres adjacentes de uma onda estacionária sobre uma corda é igual a 15,0 c m . Uma partícula situada em um ventre oscila com M H S com amplitude igual a 0,850 c m   e período igual a 0,0750 s . A corda está sobre o eixo O x e se encontra fixa no ponto x = 0 .

  1. Qual a distância entre nós adjacentes?
  2. Qual o comprimento de onda, a amplitude e a velocidade de duas ondas progressivas que adquirem essa configuração?
  3. Calcule as velocidades transversais máxima e mínima de um ponto do ventre.
  4. Qual é a menor distância ao longo da corda entre um nó e um ventre?

Passo 1

Letra a)

A distância entre nós adjacentes é a mesma distância entre dois ventres adjacentes, então x = 15 c m

Além disso, a distância entre nós adjacentes vai ser metade do comprimento da onda!

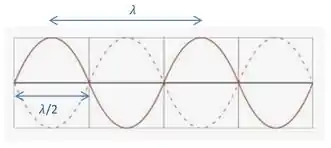
Portanto,

λ 2 = 15 c m

λ = 30 c m

Passo 2

Letra b)

Para ondas progressivas, a ideia é a mesma:

λ 2 = 15 , ou seja, λ = 30 c m = 3,0 × 10 - 1 m .

E como sabemos o período T = 0,075 s , podemos calcular a velocidade através da fórmula:

v = λ f = λ T = 3,0 × 10 - 1 0,075 = 4 m / s

A amplitude vai ser a metade da onda fornecida:

A = 1 2 0,85 = 0,43 c m = 4,3 × 10 - 3 m

Passo 3

Letra c)

A velocidade transversal vai ser a derivada temporal da função de onda:

∂ y ∂ t = v y = A ω s e n k x   c o s ω t

E vai ter valor máximo em v y = A ω e mínimo v y = 0 .

Para determinar o valor máximo precisamos do valor de ω :

ω = 2 π T = 2 π 0,075 = 83,8 r a d / s

Então

v y , m á x = 0,85 × 10 - 2 . 83,8 = 0,71 m / s

v y , m í n = 0

Passo 4

Letra d)

A distância entre um nó e um ventre adjacentes vai ser um quarto do comprimento de onda:

d = λ 4 = 30 4 = 7,5 c m = 7,5 × 10 - 2 m

Resposta

a )   15 c m

b )   30 c m , 0,43 c m ,   4 m / s

c ) v y , m á x = 0,64 × 10 - 2 . 83,8 = 0,71 m / s

v y , m í n = 0

d ) 7,5 c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é (a) a menor frequência, (b) a segunda menor frequência e (c) a terceira menor frequência das ondas estacionárias em um fio com 10,0m de comprimento, 100g de massa e 250N de tensão?
Duas ondas senoidais com comprimentos de onda e amplitudes iguais se propagam em sentidos opostos em uma corda com uma velocidade de 10c m / s . Se o intervalo de tempo entre os instantes nos quais a
Se uma linha de transmissão em um clima frio fica coberta de gelo, o aumento do diâmetro leva à formação de vórtices no vento que passa. As variações de pressão associadas aos vórtices podem fazer a l
Uma corda fixa nas duas extremidades tem 8,40m de comprimento, uma massa de 0,120k g e uma tensão de 96,0N . (a) Qual é a velocidade das ondas na corda? (b) Qual é o maior comprimento de onda possível
Uma corda com 125c m de comprimento tem uma massa de 2,00g e uma tensão de 7,00N . (a) Qual é a velocidade de uma onda na corda? (b) Qual é a frequência de ressonância mais baixa da corda?