Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.Problemas Adicionais - Ex. 102
A distância entre duas estações de metrô é . Se um trem acelera a a partir do repouso na primeira metade da distância e desacelera a na segunda metade, quais são (a) o tempo de percurso entre as estações e (b) a velocidade máxima do trem? (c) Desenhe os gráficos de , , e em função de para o percurso entre as duas estações.
Passo 1
Para resolver este problema separaremos a questão em duas partes. Primeiro analisaremos a parte com aceleração de e, em seguida, analisaremos a segunda parte do movimento.
É importante perceber que ambos são MRUV, então as funções que determinam o movimento são as mesmas a menos das constantes. Para eles usaremos:
Passo 2
Analisando a primeira parte do movimento, o enunciado diz que o trem parte do repouso (), que ele percorre uma distância , partindo de , pois consideramos o referencial no início do movimento do trem e a aceleração dessa primeira metade . Substituindo esses dados na equação acima:
Isolando :
Portanto, o trem gasta para alcançar a metade do caminho até a próxima estação.
Passo 3
Como nessa primeira parte o movimento é acelerado, então a velocidade máxima será no instante final da primeira etapa, então usando a função da velocidade no instante , temos:
Substituindo o valor de encontrado no passo anterior:
Passo 4
Para terminar de calcular o tempo que leva para chegar na outra estação, vamos dar um pulo do gato. Como o trem parte do repouso e acelera durante um deslocamento igual ao que ele desacelera com a mesma aceleração, então o tempo que o trem leva para chegar na primeira metade é o mesmo da segunda metade, então:
Passo 5
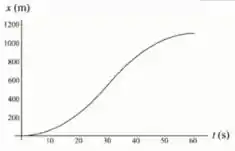
Os gráficos referentes respectivamente a posição, a velocidade e a aceleração são do tipo:
Resposta
- ;
- .