Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 2.Exercícios e Problemas - Ex. 17

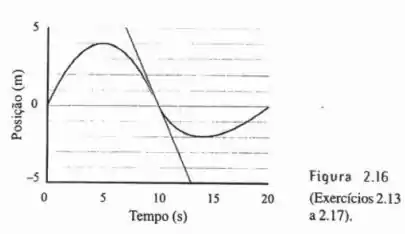
Esboce gráficos da velocidade e da aceleração, em função do tempo, do corpo cujo movimento é mostrado na figura 2.16.

Passo 1

Meus queridos e minhas queridas!

Apesar de parecer um pouco complicada, essa questão é bastante simples.

Vamos nos atentar aos aspectos da curva no intervalo [0, 10].

O que podemos perceber? Que ela possui concavidade para baixo, possui comportamento parabólico (função do segundo grau), começa da origem e no ponto máximo possui coordenadas ( x v ,   y v ) = ( 5 ,   4 ) .

Isso nos garante que, pela equação:

S t = a 2 t 2 + v o t + S o

Pelo o que constatamos: a < 0 e S o = 0 .

Portanto, pode ser reescrita:

S t = v o t + a 2 t 2

Logo, sabemos que na seguinte equação:

f x = a ' x 2 + b ' x + c '

x v = - b ' 2 a '   e   y v = - ∆ 4 a '

Adequando a equação, temos:

x v = - b ' 2 a ' = - v o a   e   y v = - ∆ 4 a ' = - ∆ 2 a

Vamos aplicar os valores que sabemos:

x v = 5

5 = - v o a ⇒ v o = - 5 a

y v = 4

4 = - ∆ 2 a

4 = - ( v o 2 - 4 ∙ a 2 ∙ S o ) 2 a

4 = - ( v o 2 - 4 ∙ a 2 ∙ 0 ) 2 a

8 a = - v o 2

Agora, vamos aplicar a relação que encontramos v o = - 5 a :

8 a = - - 5 a 2

8 a = - 25 a 2

a = - 8 25 m / s 2

O gráfico da aceleração constante em função do tempo!

Ok! Descobrimos a aceleração, agora nos resta descobrir a velocidade!

Sabemos que:

v t = v o + a t

Queremos saber v ( 10 ) e sabemos os valores de v 0   e   a !

Eu prometi que seria simples.

v t = - 5 a + a t

v t = 8 5 - 8 25 t

O gráfico da velocidade em função do tempo acima!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Partindo de uma estação, um trem de metrô acelera a partir do repouso à taxa constante de 1,00 m/s² na metade do percurso até a estação seguinte, e depois freia à mesma taxa no resto do percurso. A di
Um corredor, viajando com a rapidez constante de 125 km/h, passa por um cartaz. Um carro-patrula parte do repouso, com aceleração constante de (80 km/h)/s até atingir sua rapidez máxima de 190 km/h, q
Um trem parte de uma estação com uma aceleração constante de 0,40 m/s². Uma passageira chega a um ponto junto ao trilho 6,0 s após o final do trem ter passado pelo mesmo ponto. Qual é a menor rapidez
Uma gazela está correndo em linha reta ( oe i x ox ). O gráfico na Figura 2.45 mostra a velocidade desse animal em função do tempo. Nos primeiros 12,0s , determine a) A distânciatotal percorrida e b)
Um próton se move ao longo do eixo x de acordo com a equação x=50 t+10 t 2 , em que x está em metros e t está em segundos. Calcule (a) a velocidade do próton durante os primeiros 3,0s do percurso, (b)