Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 2.Problemas - Ex. 05
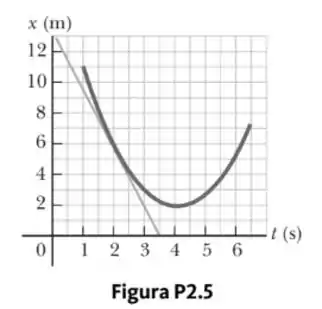
Um gráfico posição-tempo para uma partícula movendo-se ao longo do eixo x é mostrado na Figura P2.5.
- Encontre a velocidade média no intervalo de tempo t = 1,50 s a t = 4,00 s.
- Determine a velocidade instantânea em t = 2,00 s medindo a inclinação da linha tangente mostrada no gráfico.
- Em qual valor de t a velocidade é zero?
Passo 1
a.Então, galera, a velocidade média pode ser determinada a partir de gráficos posição versus tempo pela relação , onde é o deslocamento entre posições e é o intervalo de tempo percorrido no deslocamento.
Pra esse caso, verificando no gráfico, a gente vai ter:
Pra :
Pra :
Com isso, a velocidade média vai valer:
O sinal negativo indica que o corpo está se deslocando no sentido convencionado negativo do percurso. Isso fica claro no gráfico pelos intervalos em que a curva é decrescente!
Passo 2
b.A velocidade instantânea em , como foi indicado, vai ser dada pela inclinação da reta que tangencia a curva no ponto com esse valor de .
A inclinação da reta é, também, exatamente , que a gente calcula contabilizando pelo gráfico.
Nesse caso, nos baseando no triângulo retângulo que a reta tangente faz com o gráfico, vamos ter:
Pra :
Pra :
E, assim, chegamos à velocidade média de:
Passo 3
c.A velocidade vai ser nula nos pontos em que valer zero. Pra isso, precisa se anular.
Observando o gráfico, o único ponto em que vem a zerar é no ponto de mínimo, em .
Nesse ponto, o corpo para um movimento que seguia em um sentido e recomeça o movimento no sentido contrário.
Resposta
a.b.c.