Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 16.Exercício - Ex. 34
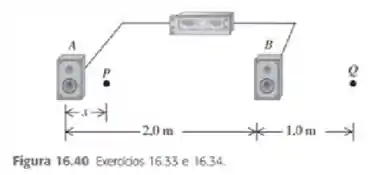
Dois alto falantes A e B (Figura 16.40), são alimentados por um mesmo amplificador e emitem ondas senoidais em fase. O alto-falante B está a uma distância de à direita do alto-falante A. os dois alto-falantes emitem ondas sonoras com uma frequência igual a e a velocidade do som no ar é igual a . Considere um ponto P ao longo da linha reta que une os dois alto-falantes e situado entre os alto-falantes a uma distância à direita do alto falante A. os dois alto-falantes emitem ondas sonoras que se propagam diretamente dos alto-falantes até o ponto P. a) quais são os valores de em que ocorre interferência destrutiva no ponto P? b) Quais são os valores de em que ocorre interferências construtiva no ponto P? c) Os efeitos de interferência como aqueles que você encontrou nos itens (a) e (b) quase nunca são ouvidos no equipamento de som estereofônico da sua casa. Por quê?
Passo 1
Bom, a questão pede para encontrarmos o valor de que é a distancia entre o alto-falante A e o ponto P, para quando a interferência é destrutiva e construtiva, ou seja, vamos mover o ponto P até exatamente o valor de x em que acontecem as interferências. Como a distância entre os dois alto-falantes é e o ponto P está entre eles, então a equação para interferência construtiva que era:
Se torna:
Pois será o caminho que a onda do alto-falante B percorre até o ponto P, e é o caminho que a onda do alto-falante A percorre até o ponto P. Como precisamos fazer a diferença entre os caminhos, é:
E o mesmo vale para a equação de interferência destrutiva:
Passo 2
a) Pela equação da velocidade de uma onda:
Podemos substituir o na equação de onda destrutiva:
E por fim, isolamos :
E substituímos os valores de cada letra:
Os únicos valores possíveis para são e que dão:
Para valores diferentes, o ponto P não vai estar mais entre os alto-falantes.
Passo 3
b) para interferência construtiva, usamos a equação da velocidade da onda sonora novamente, para substituir o na equação:
Isolando , ficamos com:
Substituindo cada valor:
Os valores que pode assumir nesse caso são , e , para cada caso, fica:
Passo 4
(c) As interferências não são percebidas porque o som se reflete em vários objetos próximos, assim como nas paredes, chão e teto, mudando as trajetórias das ondas e fazendo com que não essas interferências não ocorram exatamente como na situação do problema .