Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 16.Problemas Desafiadores - Ex. 84

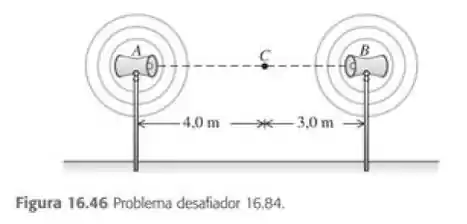
Dois alto-falantes, A e B, emitem sons uniformemente no ar, em todas as direções, a 20   ℃ . A potencia acústica emitida por A é igual a 8,0 × 10 - 4   W , e a potencia de B é igual a 6,0 × 10 - 5   W . Os dois alto-falantes estão vibrando em fase com frequência igual a 172 Hz. a)Determine a diferença de fase entre os dois sinais em um ponto C ao longo da reta que une A a B, a 3,0 m de B e 4,0 de A (Figura 16.46).b) Determine a intensidade e o nível da intensidade sonora no ponto C devido ao alto-falante A quando o alto-falanta B é desligado.c) Quando os dois alto-falantes estão ligados, calcule a intensidade e o nível da intensidade sonora no ponto C.

Passo 1

À distância r de uma fonte pontual com potência   P ,

I = P 4 π r 2 .

β = 10 d B log ⁡ I I 0 .

Para duas fontes, as amplitudes são combinadas de acordo com a diferença de fase.

A amplitude é proporcional à raiz quadrada da intensidade. Tomando a velocidade do som

344   m / s , o comprimento de onda das ondas emitidas por cada alto-falante é de 2,00   m .

Passo 2

  1. O ponto C é dois comprimentos de onda do alto-falante A e um e meio do alto-falante B e, portanto, a diferença de fase é 180   ° = π   r a d .

    2. Passo 3

  2. I = P 4 π r 2 = 8,00 × 10 - 4   W 4 π 4,00   m 2 = 3,98 × 10 - 6   W / m 2

    e o nível de intensidade do som é

    10 d B log ⁡ 3,98 × 10 6 - 66,0   d B .

    Repetindo com P = 6,00 × 10 - 5   W r = 3,00   m   fornece:

    I = 5,31 × 10 - 7   W / m 2   e β = 57,2   d B .

    Passo 4

  3. Com o resultado da parte (a), as amplitudes, deslocamento ou pressão, devem ser subtraídas. Ou seja, a intensidade é encontrada tomando as raízes quadradas das intensidades encontradas na parte (b), subtraindo e quadrando o diferença. O resultado é que:

I = 1,60 × 10 - 6   W /   m 2 e β = 62,1   d B .

Passo 3

Subtrair as intensidades de A e B dá

3,98 × 10 - 6 W m 2 - 5,31 × 10 - 7 W m 2 = 3,45 × 10 - 6 W m 2 .

Isso é muito diferente da intensidade correta em C.

Resposta

  1. A diferença de fase é: 180   ° = π   r a d
  2. I = 5,31 × 10 - 7   W / m 2   e β = 57,2   d B
  3. I = 1,60 × 10 - 6   W /   m 2 e β = 62,1   d B
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a razão (entre a maior e a menor) a das intensidades, ( b ) das amplitudes de pressão, ( c ) das amplitudes dos deslocamentos das partículas para dois sons cujos níveis sonoros diferem 37 d B
(a) Por qual fator a intensidade do som deve ser aumentada para que o nível da intensidade sonora aumente em 13,0 dB? (b) Explique por que você não precisa conhecer a intensidade do som original.
(a) Se dois sons diferem em 5,00 dB, determine a razão entre a intensidade do som mais alto e a do som mais baixo. (b) Se um som é 100 vezes mais intenso que outro, por quanto eles diferem no nível da
No ponto A, a 3,0 m de uma pequena fonte sonora que está emitindo uniformemente em todas as direções, o nível da intensidade sonora é 53 dB. (a) Qual é a intensidade do som em A? (b) A que distância d
O som de um trompete se propaga uniformemente no ar, em todas as direções, a 20 ºC. A uma distância de 5,0 m do trompete, o nível da intensidade sonora é 52,0 d.B. A frequência é 587 Hz. (a) Qual é a