Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.6 - Ex. 24
Dois besouros correm em um deserto plano, partindo do mesmo ponto. O besouro corre para leste e em uma direção ao norte do leste. O besouro corre em uma direção ao leste do norte e depois corre em outra direção. Quais devem ser (a) o módulo e (b) o sentido da segunda corrida do segundo besouro para que termine na mesma posição final que o primeiro besouro?
Passo 1
Primeiramente, vamos pensar no movimento realizado pelos dos besouros:
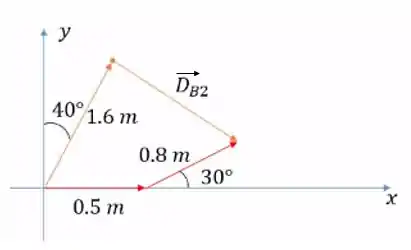
O movimento de baixo (em vermelho) é o besouro 1 e o de cima (em amarelo) é o besouro 2.
Com isso, o problema nos pede o vetor do último movimento do besouro 2 para que ele termine no mesmo lugar do besouro 1, estamos chamando esse vetor de .
Para acharmos o valor de , devemos decompor os dois movimentos de cada besouro nas coordenadas x e y e subtrair o movimento do besouro 1 pelo do besouro 2. E, depois, calculamos o módulo do vetor que encontrarmos. Vamos para a diversão!!!
Movimento do besouro 1:
Movimento do besouro 2:
Passo 2
Agora que temos os valores em cada eixo, vamos subtraí-los. Obtendo que:
E em :
Com isso, já podemos determinar o módulo pedido em (a). O módulo é calculado por:
Substituindo os valores que achamos para as componentes:
Passo 3
(b) Então, qual o sentido da segunda corrida? Queremos saber o ângulo e temos o valor dos lados do triângulo, então, usa-se uma função trigonométrica inversa que tem aí em sua calculadora. Nós temos o seguinte triângulo para o último movimento do besouro 2:
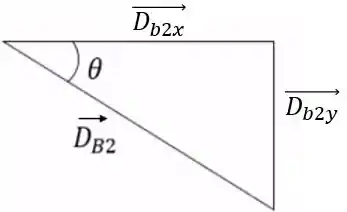
Logo:
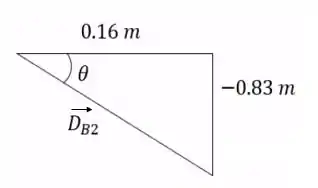
Para montar esse triângulo, é só desenhar o vetor e suas componentes, que achamos no passo anterior.
Se tirarmos a tangente do :
Ou seja, o é o ângulo, cuja tangente é . Fazendo essa conta, encontramos que:
Esse menos é só indicando que é um ângulo da horizontal para baixo. Com isso, vemos que o sentido do movimento é ao sul do leste.
Resposta
- (b) ao sul do leste