Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.Problemas - Ex. 68

Dois carros estão a de distância entre si e um se move em direção ao outro a uma velocidade constante de . Da capota de um deles, um vigoroso gafanhoto pula entre os carros (que pernas fortes ele tem!) com uma velocidade horizontal constante de em relação ao solo. O inseto pula no instante em que pousa, ou seja, não se demora sobre qualquer dos carros. Qual a distância total percorrida pelo gafanhoto antes que os carros colidam?

Passo 1

Oi, galerinha! Tudo bom? Para resolver essa questão precisamos extrair duas informações muito importantes do enunciado.

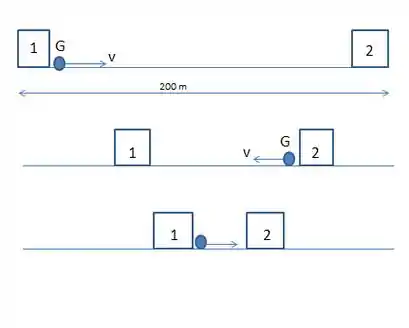
A primeira é que os carros estão vindo em sentidos opostos, então cada um vai pecorrer até se atingirem.

A segunda é que o gafanhoto tem velocidade constante de durante o tempo que leva os carros para se colidirem.

Agora vamos aos cálculos.

Passo 2

Começamos calculando o tempo até os carros colidirem:

Passo 3

Como já sabemos a velocidade do ganhoto e agora o tempo da colisão, podemos achar a distância pecorrida pelo gafanhoto:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois trens, ambos se movendo com uma velocidade de 30k m / h , trafegam em sentidos opostos na mesma linha férrea retilínea. Um pássaro parte da extremidade dianteira de um dos trens, quando estão sep

Você dirige do Rio a São Paulo metade do tempo a 55k m / h e a outra metade a 90k m / h . Na volta, você viaja metade da distância a 55k m / h e a outra metade a 90k m / h . Qual é a velocidade escala

Situação de pânico A Fig. 2 - 21 mostra uma situação na qual muitas pessoas tentam escapar por uma porta de emergência que está trancada. As pessoas se aproximam da porta com uma velocidade v s =3,50m

Em uma corrida de 1k m , o corredor 1 da raia 1 ( com o tempo de 2m i n , 27,95s ) parece ser mais rápido que o corredor 2 da raia 2 ( 2m i n ,28,15s ). Entretanto, o comprimento L 2 da raia 2 pode se

Para estabelecer um recorde de velocidade em uma distância d (em linha reta), um carro deve percorrer a distância primeiro em um sentido (em um tempo t 1 ) e depois no sentido oposto (em um tempo t 2