Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.Problemas - Ex. 85
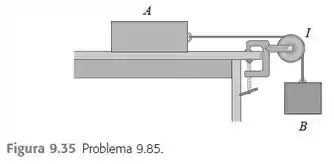
A polia indicada na Figura 9.35 possui raio R e momento de inércia I. Acorda não desliza sobre a polia e esta gira em um eixo sem atrito. O coeficiente de atrito cinético entre o bloco A e o topo da mesa é . O sistema é libertado a partir do repouso, e o bloco B começa a descer. O bloco A possui massa mA e o bloco B possui massa mB. Use métodos de conservação da energia para calcular a velocidade do bloco B em função da distância d que ele desceu.
Passo 1
E aí! Tudo certinho?
Nesse problema temos um bloco suspenso e um bloco sob uma mesa e eles estão ligados por uma corda, com isso temos que aplicar o princípio da conservação de energia para calcular a velocidade do bloco B em função da distância d que ele desceu.
Tem ideia de como fazemos isso?
Assim como sugerido no enunciado, o problema pode ser resolvido apenas usando o princípio da conservação de energia. Vamos definir o sistema de coordenadas na altura da mesa para facilitar.
Aplicando o princípio da conservação de energia, temos que:
Como o sistema inicialmente está em repouso, temos que
Além de Assumirmos que , visto que em nenhum momento o Bloco A não abandona a mesa.
Desta forma nosso problema se resume a
Veja só!
Passo 2
Devemos agora entender quem são nossas energias:
e
é importante atentar que o sistema como um todo está ligado, possuindo assim um vínculo em suas velocidades. Desta forma temos que:
e
Desta forma se resume a
Outra consideração que temos que ter é que
O Trabalho perdido no sistema , é devido ao atrito que a massa A faz com a mesa. Lembrando que a Força de atrito é devida ao contato realizada pela Força Normal, podemos escrever como:
Tranquilo até aqui?
Passo 3
Por fim podemos escrever nossas relações como
Agora fica por conta de isolarmos o
E aí! O que achou? Responde Aí!
Resposta
A velocidade final em função da distância é