Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.Problemas - Ex. 86
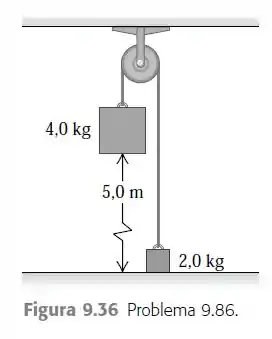
A polia indicada na Figura 9.36 possui raio 0,160 m e momento de inércia . A corda não desliza sobre a periferia da polia. Use métodos de conservação da energia para calcular a velocidade do bloco de 4,0 kg no momento em que ele atinge o solo.
Passo 1
E aí! Tudo certinho?
Entãaoo, vamos juntos nessa! Se liga:
Vamos tomar a energia potencial de cada bloco ser zero em sua posição inicial. A energia cinética do sistema é a soma das energias cinéticas de cada objeto.
Na polia, sabemos que , onde é a velocidade comum dos blocos e é a velocidade angular da polia.
Veja só!
Passo 2
Olhando para o bloco de 4kg:
Logo, pela segunda Lei de Newton, a força resultante sobre esse bloco será a diferença dos dois pesos:
Bom, antes de entrar em movimento, o bloco possui apenas a energia potencial gravitacional relacionada à força (diferença dos pesos):
Então, quando o bloco entrar em movimento, toda essa energia potencial gravitacional começará a se transformar em energia cinética. E isso vai acontecer até o bloco antigir o solo, ou seja, até não ter mais energia pontecial para transformar em cinética.
Podemos dizer, então, que no útimo instante de movimento (ao atingir o solo), por conservação de energia, toda essa energia potencial virará cinética.Com isso, esperamos que a energia cinética final seja:
Tranquilo até aqui?
Passo 3
Então, vamos analisar como vai ficar essa energia cinética no final de tudo, beleza??
Em termos da velocidade comum dos blocos, a energia cinética do sistema é:
Sendo a energia cinética associada ao movimento dos blocos e , à rotação da polia:
E colocando em evidência,
Isso implica que:
Só que vimos que, no último instante, a energia cinética total vale :
Ufa! Conseguimos! Entendeu tudo? Responde Aí!