Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.9 - Ex. 73
Dois navios, e , deixam o porto ao mesmo tempo . O navio navega para noroeste a nós e o navio navega a nós em uma direção a oeste do sul. ( nó milha marítima por hora; veja o Apêndice D.) Quais são (a) o módulo e (b) a orientação da velocidade do navio em relação ao navio ? ( c) Após quanto tempo os navios estarão separados por milhas marítimas? (d) Qual será o curso de (orientação do vetor posição de ) em relação a nesse instante?
Passo 1
Então pessoal , como e , como mostra a figura a seguir, os vetores velocidade (em relação à margem) dos navios e são dados por:
Com e , temos:
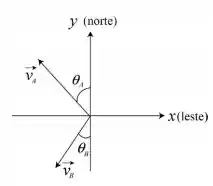
A gente sabe que a velocidade do navio em relação ao navio é dada por .
Passo 2
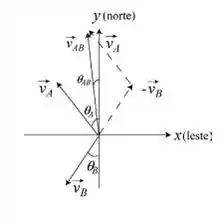
Show de bola então pessoal, a velocidade relativa é dada por:
Nós podemos achar o módulo como de costume, através da relação:
Ou seja, o módulo é de aproximadamente !
Passo 3
Para acharmos o ângulo que faz com o norte , por sua vez , usando a trigonometria básica sabemos que pode ser obtido através da relação:
Ou seja, a vetor aponta a a leste do norte .
Passo 4
Como os dois navios deixaram o porto ao mesmo tempo, a velocidade relativa descreve a taxa com a qual a distância entre os navios está aumentando. Como essa taxa é constante, temos:
Até aqui tranquilo? Bora continuar que já está acabando
Passo 5
Então galera , a velocidade não varia com o tempo e tem a mesma orientação que , já que os navios deixaram o porto no mesmo instante. Invertendo os pontos de vista, temos e, portanto, . Assim, concluímos que mantém um curso a oeste do sul em relação a durante toda a viagem (desprezando a curvatura da Terra).
Tranquilo pessoal ? Bora resolver mais questões então!!!!!
Resposta
Ei, a resposta está no passo a passo :)