Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.9 - Ex. 77
Um trem viaja para o sul a (em relação ao solo) em meio a uma chuva que é soprada para o sul pelo vento. As trajetórias das gotas de chuva fazem um ângulo de com a vertical quando medidas por um observador estacionário no solo. Um observador no trem, entretanto, vê as gotas caírem exatamente na vertical. Determine a velocidade escalar das gotas de chuva em relação ao solo.
Passo 1
Bom pessoal, vamos láá!!
Como as gotas de chuva caem verticalmente em relação ao trem, a componente horizontal da velocidade de uma gota, , deve ser igual à velocidade do trem, ou seja, , concorda?!
Bora dar uma olhada no esquema do problema:
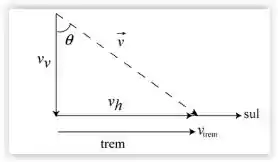
Por outro lado, se é a componente vertical da velocidade e é o ângulo entre a direção do movimento e a vertical para um observador estacionário, então temos que . Assim, conhecendo podemos determinar e conhecendo e podemos calcular a velocidade das gotas de chuva.
Passo 2
Para , a componente vertical da velocidade é:
Beleza?!
Passo 3
A velocidade das gotas de chuva conseguimos calcular usando:
Substituindo os valores, temos que:
Resposta
Tranquilo galera??? Bora resolver mais questões então!!!!