Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 11.Problemas - Ex. 4

Dois patinadores de massa 60 k g , deslizando sobre uma pista de gelo com atrito desprezível, aproximam-se um do outro com velocidades iguais e opostas de 5 m / s , segundo retas paralelas, separadas por uma distância de 1,40 m . (a) Calcule o vetor momento angular do sistema e mostre que é o mesmo em relação a qualquer ponto e se conserva (b) Quando os patinadores chegam a 1,40 m um do outro, estendemos braços e dão-se as mãos, passando a girar em torno do CM comum. Calcule a velocidade angular de rotação.

Passo 1

O vetor momento angular é moleza! Vamos pegar um eixo aqui que passa pela trajetória de um patinadores!

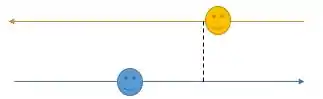
O azul, que está sobre o eixo, não tem momento angular, só o amarelo vai ter! E como é paralelo, é molinho!

L → = m r → × v →

L → = 60 k g 1.4 m 5 m s

L → = 420 k g m 2 s

Passo 2

Agora vamos conservar o momento angular, já que não teve nenhuma força externa atuando!

L = I ω

I ω = 420

Como a gente calcula o I ? Vamos considerar que são dois pontos em torno de um eixo. Daí,

I = 2 m r 2

I = 2 60 k g 0.70 m 2

I = 58.8   k g m 2

Substituindo:

ω = 420 58.8

ω = 7.1 r a d s

Resposta

L → = 420 k g m 2 s

ω = 7.1 r a d s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um certo instante, a força F → = 4 j → N age sobre um objeto de 0,25 k g cujo vetor posição é r → = 2 i → - 2 k → e cujo vetor velocidade é v → = - 5 i → + 5 k → . Em relação à origem e em termos d
No instante da figura abaixo, duas partículas se movem em um plano x y . A partícula P 1 possui uma massa de 6,5 k g e uma velocidade v 1 = 2,2 m / s e está a uma distância d 1 = 1,5 m do ponto O . A
Um objeto de 2 k g que se comporta como uma partícula, se move em um plano com componentes de velocidade v x = 30 m / s e v y = 60 m / s ao passar por um ponto de coordenadas ( 3 ; - 4 ) m . Nesse ins
No instante da figura abaixo, uma partícula P de 2 k g possui um vetor posição r → de módulo 3 m e ângulo θ 1 = 45 ° e uma velocidade v → de módulo 4 m s e ângulo θ 2 = 30 ° . A força F → , de módulo
No instante que o deslocamento de um objeto de 2 k g em relação à origem é d = 2 m i → + 4 m j → - 3 m k → , a velocidade é v → = - 6 m / s i → + 3 m / s j →+ 3 m / sk⃗ e o objeto está sujeito a uma f