Duas cascas condutoras concêntricas têm raios e , cargas uniformes e e espessura insignificante. Determine o módulo do campo elétrico E a uma distância do centro de curvatura das cascas (a) ; (b) ; (c) . Com V= O no infinito, determine V para (d) ; (e) ; (f) ; (g); (h) ; (i) . (J) Plote E(r) e V(r).

Para o item (b), lembrando que a casca envolvida agora é só a casca menor:

Agora, no item (c), não há mais nenhuma carga envolvida logo:

Agora, no item (d), temos que encontrar o potencial, temos que a formula para o potencial gerado por uma carga condutora fora da casca é:

Assim:

No item (e), como o raio da esfera 2 é igual a distância, podemos utilizar a mesma equação do item (d):

Agora, no item (f), como queremos calcular o potencial dentro de uma das esferas condutoras devemos lembrar que o potencial dentro de uma esfera condutora é constante. Dessa forma:

Aqui tem um detalhe a carga está fora da casca dela portanto o seu potencial não é constante, mas tem potencial constante.

No item (g), seguimos o raciocino do item (f):

No caso dos itens (h) e (i), devemos lembrar de novo que o potencial dentro de uma casca esférica conduta é constante, assim:

Pro gráfico vamos começar fazendo para o campo elétrico, aqui basta entendermos que:

Se:

Não há cargas na envoltória

Há apenas a carga , portanto temos uma função pro campo:

Temos a carga e a carga na envoltória e há uma descontinuidade na função nesse ponto em forma de aumento.

Se liga:

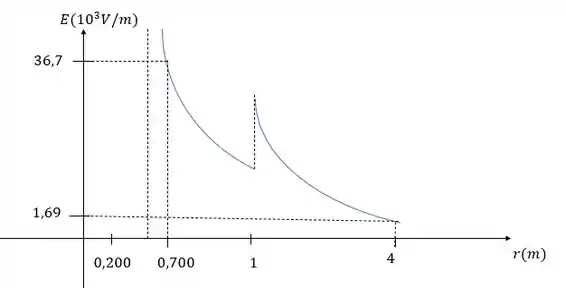
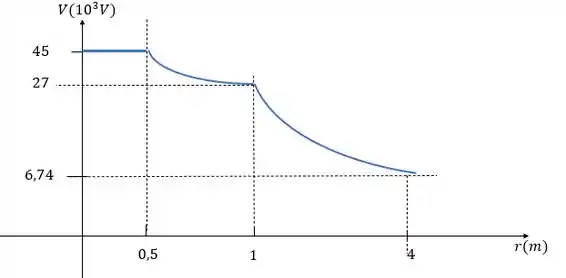
O outro gráfico também depende da distância , porém de uma maneira mais sutil lembrando que dentro das duas cascas o valor é totalmente constante, entre elas a queda é sutil e depois se torna mais acentuada.

O gráfico de tem essa carinha aqui: