Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 11
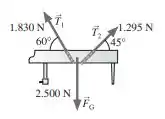
As duas cordas vistas na FIGURA EX11.11 são usadas para baixar em 5,0 m um piano de 255 kg do segundo andar de uma loja ao térreo. Quanto trabalho é realizado por cada uma das três forças?
Passo 1
O trabalho de uma força constante é dado por:
onde é o ângulo entre o vetor força e o vetor deslocamento. Assim, tendo tais valores podemos calcular o trabalho.
Passo 2
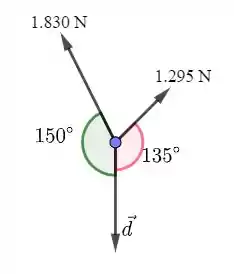
A figura abaixo representa as forças de 1.830 N e 1.295 N e seus respectivos ângulos com o vetor deslocamento. Note que a força de 2.500 N faz um ângulo de 0° com o vetor deslocamento.
Observe ainda que 60° = 60° + 90° e 135° = 45° + 90°.
Passo 3
Resposta
-7.924 J; -4.579 J e 12.500 J.
Exercícios de Livros Relacionados
Uma força horizontal única, com a orientação de +x, atua sobre um carrinho de massa m. O carrinho parte do repouso em x = 0, e sua rapidez cresce com x como v = Cx, onde C é uma constante. (a) Encontr
Uma força atuando sobre uma partícula do plano xy, nas coordenadas (x, y), é dada por F → = F 0 r y i ^ - x j ^ onde F 0 é uma constante positiva e r é a distância dapartícula à origem. (a) Mostre que
Um bloco de massa m, sobre uma mesa horizontal sem atrito, é preso a urna mola que está fixa ao teto (figura abaixo). A distância vertical entre o topo do bloco e o teto é y 0 , e sua posição horizont
Um pequeno bloco com massa de 0,120k g está ligado a um fio que passa através de um buraco em uma superfície horizontal sem atrito. Inicialmente, o bloco gira a uma distância de 0,40m do buraco com um
Um revólver de mola é engatilhado comprimindo-se uma mola, pequena e forte, de uma distância d . Ele dispara, verticalmente para cima, um sinalizador luminoso de massa m . O sinalizador tem uma rapide