Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 16

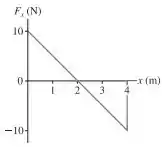
Uma partícula de 2,0 kg que se move ao longo do eixo x experimenta a força representada na FIGURA EX11.16. A velocidade da partícula em x = 0 m é de 4,0 m/s. Qual é sua velocidade em x = 2 m e 4 m?

Passo 1

Nesse exercício, vamos utilizar o teorema da energia cinética. Tal teorema nos diz que: o trabalho da força resultante é igual à variação de energia cinética da partícula. Em linguagem matemática, temos que

W = Δ E K W = E f i n a l - E i n i c i a l W = 1 2 m v f 2 - 1 2 m v i 2 W = m 2 v f 2 - v i 2

onde m é a massa; v f é a velocidade final e v i é a velocidade inicial.

Porém, devemos calcular esse trabalho. Como podemos fazer isso? Sabemos que a área sob o gráfico F × x é igual ao trabalho realizado por F . Assim, bastará calcular a área que automaticamente saberemos o trabalho :)

Porém, tome cuidado! A área é positiva quando o gráfico se localiza acima do eixo x ; e é negativa quando o gráfico se localiza abaixo do eixo x !

Passo 2

  • Para x = 2 temos o seguinte esquema

    • W = á r e a   d o   t r i â n g u l o W = b a s e × a l t u r a 2 W = 10 × 2 2 W = 10   J

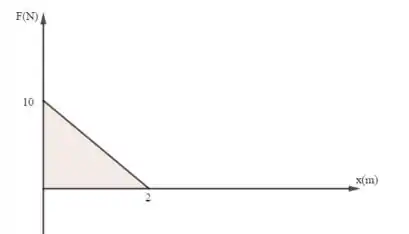
    Portanto, aplicando o teorema da energia cinética:

    W = m 2 v f 2 - v i 2 10 = 2,0 2 v f 2 - 4 2 v f 2 = 2 6 v f = 5,1   m / s

  • Para x = 4   m , temos

W = A r e a   t r i a n g u l o   1 + A r e a   t r i a n g u l o   2 W = 2 × 10 2 + 2 × - 10 2 W = 0

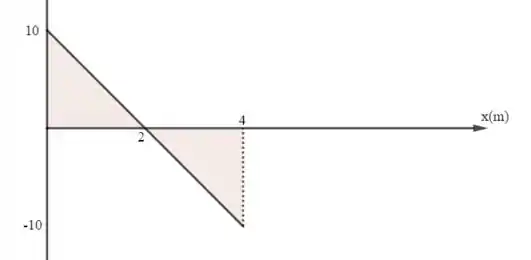
Aplicando o teorema da energia cinética,

W = m 2 v f 2 - v i 2 0 = 2,0 2 v f 2 - 4 2 v f 2 = 16 v f = 4,0   m / s

Resposta

5,1 m/s e 4,0 m/s.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pedreiro engenhoso montou um dispositivo que dispara tijolos até a altura da parede onde ele está trabalhando. Ele coloca o tijolo comprimindo uma mola vertical com massa desprezível e constante da
Um pequeno cavaleiro comprime uma mola na parte inferior de um trilho de ar inclinado de um ângulo de 40,0 ° acima da horizontal. O cavaleiro possui massa 0,0900k g . A mola possui massa desprezível e
Em um parque aquático, um trenó com seu condutor é impulsionado ao longo de uma superfície horizontal escorregadia pela liberação ao longo de uma superfície horizontal escorregadia pela liberação de u
Um carregador empurra uma mala de 20,0 kg para cima de uma rampa com inclinação de 25,0° acima da horizontal com uma força F → de módulo igual a 140 N que atua paralelamente àrampa. O coeficiente de a
Um objeto é atraído para a origem com uma força dada por F x = - k / x 2 . (As forças elétricas e as gravitacionais possuem esse tipo de dependência com a distância.) a) Calcule o trabalho realizado p