Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 18
Duas esferas condutoras isoladas de raios iguais têm cargas e , respectivamente. Os centros das esferas estão separados por uma distância , que é grande comparada ao raio delas. Estime o valor da capacitância deste capacitor não usual.
Passo 1
Cara... Antes de iniciarmos a nossa matemática, que tal desenharmos o que está acontecendo no problema?
Bem, temos duas esferas de cargas de raio pequeno comparado com a distância entre alas...
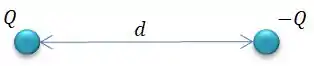
E aí o problema pede para determinarmos a capacitância desse capacitor não usual.
Ora... Você deve estar se perguntando: Isso é um capacitor?
A resposta é sim! Afinal, para termos um capacitor, bastam termos duas cargas opostas separadas por certa distância.
Se for um capacitor, tem capacitância que pode ser dada pela relação...
Onde é a diferença de potencial entre elas. Veja que então se encontrarmos esse potencial, o problema vai estar resolvido, afinal queremos a capacitância e daí, com em mãos, bastará...
Partiu vermos melhor quem é o ?
Passo 2
Como acabamos de conversar, é a diferença de potencial entre as duas esferas de cargas...
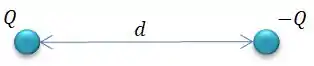
De acordo com a nossa teoria, o potencial eletrostático de uma esfera de cargas pode ser dado por...
Onde é a distância do centro da esfera ao ponto onde se quer medir o potencial da esfera...
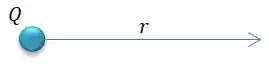
POW! Como queremos medir o potencia até a posição do centro da outra esfera de carga...
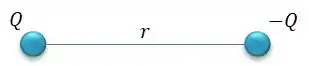
Podemos considerar o potencial entre as duas esferas então como...
Afinal... , saca?
Todavia, contudo, não obstante... , então podemos considerar ... Então...
Passo 3
“Tá! Mas não queremos o potencial entre as esferas e sim a capacitância entre elas”.
Correto! Mas do passo ...