Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 75
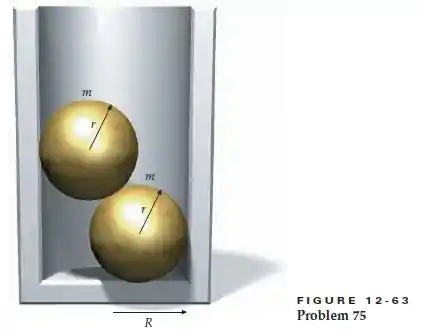
Duas esferas maciças e polidas (sem atrito), de raio r, são colocadas dentro de um cilindro de raio R, como na Figura 12-63. A massa de cada esfera é m. Determine a força exercida pela base do cilindro sobre a esfera de baixo, a força exercida pela parede do cilindro sobre cada esfera e a força exercida por uma esfera sobre a outra. Expresse todas as forças em termos de m, R e r.
Passo 1
Bom, vamos com muita calma ! Primeiro desenhamos o sistema e acrescentamos as forças. Supondo que a direção y seja positiva para cima e x positivo para a direita:
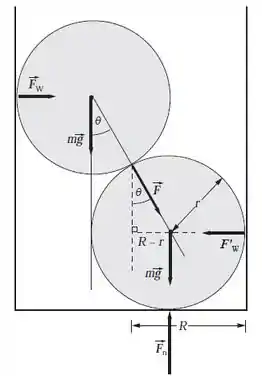
A gente percebe que quando uma bola esta em contato com a outra a de cima irá exercer uma força sobre a de baixo (), formando com a força peso da superior um ângulo (). A parede exerce força sobre a bola superior () e na inferior (). Para finalizar existe um contato entre a bola inferior e a base do cilindro ().
E o que queremos neste problema? Todas elas !
Vamos começar lembrando que todo o sistema se encontra em equilíbrio, neste caso as condições são válidas. Vamos começar usando .
Se , então .
Na direção x, nós temos as forças peso e a normal da base sobre a bola. A força F não será considerada na equação porque ela é a composição da força peso da primeira bolinha. Jogando na fórmula:
Legal, já achamos uma das forças !
Passo 2
Acabei de dizer no passo 1 que a força é a composição da força peso, que formam um ângulo com a mesma.
Por trigonometria:
Isolando:
O problema nos pediu para relacionar as forças com m, R e r, não em relação ao ângulo. Então vamos achar o ângulo em função disso.
Podemos observar que o ângulo faz parte de um triângulo retângulo:
Queremos achar cosseno, mas não temos o cateto adjacente, então vamos usar:
Então:
Também podemos achar o seno:
Só precisamos substituir isso na força:
Passo 3
O último passo é achar a força com que a parede do cilindro exerce sobre a bola. Para fazer isso podemos usar
Na direção x temos as forças da parede sobre as bolas, em direções opostas, como as características destes dois sistemas são iguais podemos assumir que:
A outra força que atua nesta direção é a força peso na direção x:
Substituindo F, obtido do passo 2, e o seno:
Jogando em :
Pronto, achamos todas as forças que queríamos!