Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 16.1 - Ex. 39
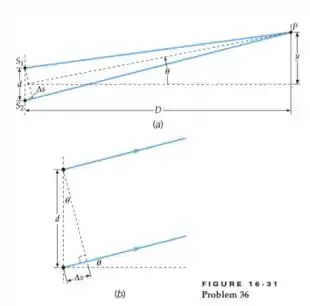
Duas fontes de som acionadas em fase pelo mesmo amplificador estão separadas por no eixo y, uma em e a outra em . Em pontos de grandes distâncias do eixo y, é ouvida uma interferência construtiva em ângulos com o eixo x de , e e sem ângulos intermediários (veja Figura 16-31) (a) Qual é o comprimento de onda das ondas sonoras das fontes? (b) Qual é a frequência das fontes? (c) Em que outros ângulos a interferência construtiva é ouvida? (d) Qual é o menor ângulo para o qual as ondas sonoras cancelam?
Passo 1
No item (a), precisamos usar a equação de interferência construtiva:
E então calcularmos o com um dos ângulos dados no enunciado, podendo ser qualquer um já que o comprimento de onda não varia para cada ângulo, vamos usar :
Substituindo os valores:
Passo 2
Com o resultado de (a), podemos calcular o (b) pela equação de velocidade da onda:
Isolando
Substituindo os valores:
Passo 3
Na (c), montaremos uma tabela para cada um dos m e dos seus respectivos pela equação dos máximos:
E a tabela vai ficar:
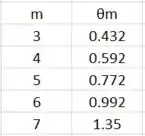
Para valores maiores que 7 o arco seno é indefinido.
Passo 4
E a letra (d) pede o primeiro mínimo em termos do ângulo, para isso vamos usar a equação dos mínimos:
Como é o primeiro, m=1, e ficamos com:
Resolvendo para