Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 107
Duas hastes finas, uniformes e idênticas, cada uma de comprimento , estão coladas nas extremidades uma da outra de forma que o ângulo na junção é de . Determine a localização do centro de massa (em termos de ) dessa configuração em relação a uma origem situada na junção. Dica: você não precisa da massa das hastes, mas você deve começar assumindo uma massa e verificar que ela se cancela.
Passo 1
Vamos começar fazendo um esquema da situação:
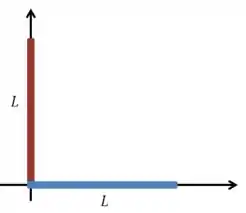
E para cada haste o centro de massa está situado no ponto médio, então as coordenadas são:
Passo 2
Agora vamos calcular as coordenadas do centro de massa em cada eixo, considerando que a massa de cada haste é :
Resposta
As coordenadas do centro de massa são .
Exercícios de Livros Relacionados
Em uma escavação arqueológica de fim de semana, você descobre um antigo martelo que consiste de uma pedra simétrica de 8,0k g presa na ponta de um pedaço de madeira uniforme de 2,5k g . Você mede as d
Três bolas, A , B e C , com massas 3,0k g , 1,0k g e 1,0k g , respectivamente, estão conectadas por hastes sem massa, como mostrado na figura. Quais são as coordenadas do centro de massa do sistema.
Por simetria, localize o centro de massa de uma folha uniforme em forma de triângulo equilátero com lados de comprimento a . O triângulo tem um vértice no eixo y e os outros em ( - a 2 , 0 ) e ( + a 2
Uma lata em forma de cilindro simétrico de massa M e altura H está cheia de água. A massa inicial da água é M , mesma massa da lata. Um pequeno buraco é feito no fundo da lata, e a água começa a escor