Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 102
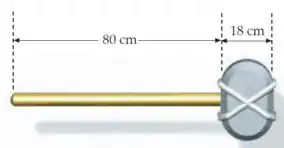
Em uma escavação arqueológica de fim de semana, você descobre um antigo martelo que consiste de uma pedra simétrica de presa na ponta de um pedaço de madeira uniforme de . Você mede as dimensões do martelo conforme mostrado na figura. Qual a distância entre o centro de massa do martelo e a ponta por onde se empunha o martelo?
Passo 1
a) Falaa, querido! Ele quer a posição do centro de passa dessa peça em relação a sua extremidade esquerda. Tem um passo a passo para resolver questões de centro de massa. É seguir ele que dá bom!
Primeira coisa é achar a posição do centro de massa de cada uma das partes. Mas precisa ser em relação a um ponto determinado. Como ele pede o centro de massa da peça em relação a extremidade esquerda, vamos colocar a origem do nosso eixo lá.
Tanto o cabo quando a pedra são homogêneos, então o centro de massa de cada um deve estar localizado no ponto médio dos seus respectivos comprimentos.
Vamos supor que a pedra tem um furo, e que o bastão passa por dentro dela, de forma que o comprimento total do cabo é .
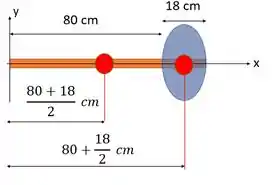
A gente só colocou ai para marcar a origem de . Aí queremos a distância entre e o centro de massa do cabo, que vai ser metade do seu comprimento:
E queremos a distância entre e o centro de massa da pedra, que vai ser metade do seu comprimento mais a distância entre a pedra e o eixo :
Passo 2
E agora para calcular a posição do centro de massa em relação ao nossa origem, só precisamos calcular a média ponderada das posições em relação a massa de cada parte. Basicamente, é usar essa fórmulinha:
Onde é a massa de uma parte da nossa peça e é a distância entre o centro de massa dessa parte e . é a massa tota da peça. é a soma dos produtos . Para o nosso caso, essa fórmulinha fica:
Substituindo os dados:
Resposta
O centro de massa do martelo está a da ponta.