Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 34.Problemas - Ex. 96
Duas lentes de contato. (a) Prove que, quando duas lentes delgadas com distâncias focais e estão em contato, a distância focal da combinção é dada por
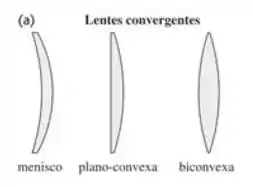
(b) Uma lente menisco convergente (Figura 34.32a) possui índice de refração igual a e suas superficies apresentam raios de curvatura de e . A superfície côncava é colocada para cima e cheia com tetracloreto de carbono (), com . Qual é a distância focal da combinação ?
Passo 1
Vamos começar escrevendo uma equação para a distância focal de cada lente:
O que vai acontecer aqui é o seguinte: o objeto vai estar na posição , e depois de passar pelas duas lentes vai gerar uma imagem na posição .
Então a distância focal da combinação segue essa fórmula aqui:
Mas tem um detalhe! Já que as duas lentes estão em contato, a gente pode afirmar o seguinte:
Ou seja, a imagem da primeira lente serve de objeto pra segunda. Como as lentes estão em contato, a posição só troca de sinal quando estamos passando do referencial de uma lente pra outra.
Passo 2
Então vamos lá. Reescrevendo o sistema com essa última informação, a gente fica com o seguinte:
Agora vamos somar as duas equações:
E esse termo aí na esquerda é exatamente a definição do que a gente escreveu lá em cima:
Pronto! Demonstramos a fórmula do enunciado.
Passo 3
(b) Tá, aqui claramente a gente vai ter que aproveitar a fórmula do item (a):
Mas antes temos que calcular as distâncias focais de cada uma das lentes. A fórmula que vamos usar pra isso é essa aqui:
Então, começando pelo vidro, ficamos com:
E para o tetracloreto de carbono:
O que acontece aí é, quando a superfície côncava é “cheia” com o tetracloreto, ela passa a se comportar como uma superfície plana, por isso o raio de curvatura se torna infinito.
Resolvendo a expressão:
Passo 4
Agora é só substituir os valores na fórmula de cima:
Resposta
(a) Demonstração.
(b) A distância focal da combinação é .