Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 16.1 - Ex. 35

Duas ondas de água harmônicas de amplitudes iguais, mas frequências, números de ondas e velocidades diferentes estão viajando na mesma direção. Além disso, elas são sobrepostos. O deslocamento total da onda pode ser escrito como y   ( x ,   t ) = A   [ c o s   ( k 1 x -   ω 1 t )   +   c o s ( k 2 x - ω 2 t ) ] , onde ω 1 / k 1 = v 1 (a velocidade da primeira onda ) e ω 2 / k 2 = v 2 (a velocidade da segunda onda). (a) Mostre que y   ( x ,   t ) pode ser escrito na forma y   ( x ,   t )   =   Y   ( x ,   t )   c o s   ( k m x - ω m t ) ,   onde ω m = ( ω 1 + ω 2 ) / 2 , k m =   ( k 1 + k 2 ) / 2 , Y   ( x ,   t )   =   2 A   c o s   [ ( Δ k / 2 ) x   -   ( Δ ω / 2 ) t ] , Δ   ω = ω 1 - ω 2 e Δ k   =   k 1 - k 2 . O fator Y   ( x ,   t ) é chamado de envelope da onda. (b) Seja A   =   1,00   c m , ω 1 =   1,00   r a d / s , k 1   =   1,00 m - 1 , ω 2 = 0,900   r a d / s , e k 2 = 0,800 m - 1 . Usando um programa de planilha ou calculadora gráfica, faça um gráfico de y   ( x ,   t ) versus x em t   =   0,00   s por 0   < x   < 5,00   m . (c) Usando um programa de planilha ou calculadora gráfica, faça três gráficos de Y   ( x ,   t ) versus x para - 5,00   m   < x   < 5,00 m no mesmo gráfico. Faça um gráfico para t   =   0,00   s , o segundo para t   =   5,00   s e o terceiro para t   =   10,00   s . Estime a velocidade com que o envelope se move das três parcelas e compare esta estimativa com a velocidade obtida usando v e n v e l o p e = Δ ω / Δ k .

Passo 1

(a)Bom, precisamos reescrever a equação das ondas:

y   ( x ,   t ) = A   [ c o s   ( k 1 x -   ω 1 t )   +   c o s ( k 2 x - ω 2 t ) ]

Em termos de uma função   Y   ( x ,   t ) :

Y   ( x ,   t )   =   2 A   c o s   [ ( Δ k / 2 ) x   -   ( Δ ω / 2 ) t ]

Para isso, vamos usar a seguinte identidade trigonométrica:

c o s A + c o s B = 2 cos ⁡ A + B 2 cos ⁡ A - B 2

Na primeira equação, ficamos com:

y   ( x ,   t ) = 2 A   c o s   k 1 x -   ω 1 t + k 2 x - ω 2 t 2 c o s k 1 x -   ω 1 t - k 2 x + ω 2 t 2

y   ( x ,   t ) = 2 A   c o s   k 1 + k 2 2 x - ω 1 + ω 2 2 t c o s k 1 - k 2 2 x - ω 1 - ω 2 2 t

Passo 2

E agora substituindo ω m = ( ω 1 + ω 2 ) / 2 , k m =   ( k 1 + k 2 ) / 2 , Δ   ω = ω 1 - ω 2 e Δ k   =   k 1 - k 2 , a equação fica:

y   ( x ,   t ) = 2 A   c o s   k m x - ω m t c o s   Δ k 2 x -   Δ   ω 2 t

E então:

y   ( x ,   t ) = Y   ( x ,   t ) c o s   k m x - ω m t  

Passo 3

Na letra (b), os valores utilizados para cada uma das grandezas na equação foram:

k 1 = 1   m - 1

k 2 = 0.8   m - 1

A = 1   m

E t = 0.00 s , que foi pedido no enunciado. O seguinte gráfico foi plotado para 0.00 ≤ x ≤ 5.00 :

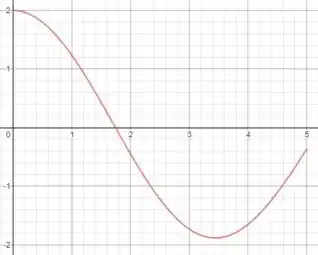
Passo 4

E na (c), usaremos os seguintes valores:

A = 1   m

Δ k = 0.2   m - 1

Δ ω = 0.1   s - 1

Os gráficos para cada tempo pedido no enunciado ficarão assim:

Sendo a curva azul para t = 0.00 s , a curva vermelha t = 5.00 s e a curva laranja t = 10.00 s

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas ondas se propagam na mesma corda: y 1 x , t = 4,60m m sen ⁡ ( 2 π x - 400 π t ) y 2 x , t = 5,60m m sen ⁡ ( 2 π x - 400 π t + 0,80 πr a d ) Qual é (a) a amplitude e (b) o ângulo de fase (em relaç
Duas ondas senoidais de mesma frequência e mesmo sentido são produzidas em uma corda esticada. Uma das ondas tem uma amplitude de 5,0m m e a outra uma amplitude de 8,0m m . (a) Qual deve ser a diferen
Duas ondas são descritas por: y 1 = 0,30 s e n [ π ( 5 x - 200 t ) ] y 2 = 0,30 s e n [ π 5 x - 200 t + π 3 ] Onde y 1 , y 2 e x estão em metros e t está em segundos. Quando as duas ondas são combinad
Duas ondas harmônicas propagam-se em uma corda no mesmo sentido, ambas com uma frequência de 100H z , um comprimento de onda de 2,0c m e uma amplitude de 0,020m . Ademais, elas se sobrepõem. Qual é a
Dois alto-falantes, colocados face a face, oscilam em fase com a mesma frequência. Eles estão separados de uma distância igual a um terço de um comprimento de onda. O ponto P está em frente aos dois a