Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.6 - Ex. 37

Duas ondas se propagam na mesma corda:

y 1 x , t = 4,60   m m sen ⁡ ( 2 π x - 400 π t )

y 2 x , t = 5,60   m m sen ⁡ ( 2 π x - 400 π t + 0,80 π   r a d )

Qual é (a) a amplitude e (b) o ângulo de fase (em relação à onda 1 ) da onda resultante? (c) Se uma terceira onda de amplitude 5,00   m m também é produzida na corda com o mesmo sentido que as duas primeiras, qual deve ser o ângulo de fase para que a amplitude da nova onda resultante seja máxima?

Passo 1

Falaa galerinha do RespondeAí, tudo beleza?

Nesse exercício aqui, o enunciado nos deu a função de onda de duas ondas que se propagam na mesma corda, dadas como:

y 1 x , t = 4,60   mm sen ⁡ 2 π x - 400 π t

y 2 x , t = 5,60   mm sen ⁡ ( 2 π x - 400 π t + 0,80 π   rad )

Sabendo disso, na letra (a), o enunciado pede pra gente encontrar a amplitude do movimento.

Vamos começar representando as duas ondas em um diagrama de fasores:

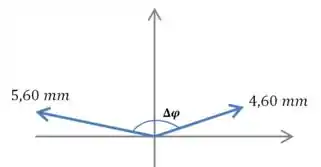
Lembre que os fasores estão girando no plano em torno da origem. A diferença de fase entre eles é:

Δ φ = 0,80 π

∆ φ = 144 °

Passo 2

Iradoso, então pra gente encontrar a onda resultante da interferência entre essas duas ondas, podemos somar vetorialmente esses fasores. Vamos desenhar um esquema dessa soma:

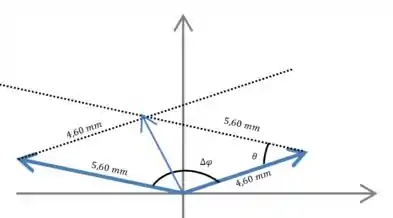
Belezoca, como os ângulos internos do quadrilátero somam 2 π e os ângulos opostos são iguais, a gente consegue descobrir o valor daquele θ , tal que:

2 π = 2 0,80 π + 2 θ

π = 0,80 π + θ

Logo:

θ = 0,20 π

E pela lei dos cossenos o comprimento do fasor resultante será:

Y m 2 = 5,6 2 + 4,6 2 - 2 5,6 4,6 c o s ⁡ ( 0,20 π )

Y m = 10,83

Y m = 3,29   mm

Prontinho.

Passo 3

Show de bolinhas, agora na letra (b) queremos a diferença de fase entre o vetor resultante e o vetor y 1 .

Vamos usar a lei dos cossenos de novo, naquele mesmo triângulo de antes, mas dessa vez, para encontrar o ângulo que representa essa diferença de fase, de modo que:

5,60 2 = 3,29 2 + 4,60 2 - 2 3,29 4,60 . c o s ⁡ ( Δ ϕ )

Sendo assim

cos ⁡ Δ ϕ = 0,020619

Δ ϕ = 1,55   rad

Passo 4

Maravilha, por fim na letra (c) queremos adicionar uma terceira onda, de amplitude y 3 = 5,00   mm , de forma a maximizar a amplitude da onda resultante.

A malandragem aqui é que o ângulo de fase tem que estar exatamente em cima do vetor resultante que já calculamos, porque dessa forma a amplitude resultante vai ser a maior possível, afinal qualquer outra posição levaria a uma amplitude menor.

Logo, a resposta é o valor que acabamos de calcular:

Δ α = 1,55   rad

Resposta

(a) Y m = 3,29   mm

(b) Δ ϕ = 1,55   rad

(c) Δ α = 1,55   rad

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas ondas são descritas por: y 1 = 0,30 s e n [ π ( 5 x - 200 t ) ] y 2 = 0,30 s e n [ π 5 x - 200 t + π 3 ] Onde y 1 , y 2 e x estão em metros e t está em segundos. Quando as duas ondas são combinad
Duas ondas harmônicas propagam-se em uma corda no mesmo sentido, ambas com uma frequência de 100H z , um comprimento de onda de 2,0c m e uma amplitude de 0,020m . Ademais, elas se sobrepõem. Qual é a
Dois alto-falantes, colocados face a face, oscilam em fase com a mesma frequência. Eles estão separados de uma distância igual a um terço de um comprimento de onda. O ponto P está em frente aos dois a
Duas ondas harmônicas de mesma frequência, rapidez de onda e amplitude propagam-se no mesmo sentido e no mesmo meio de propagação. Ademais, elas se sobrepõem. Se elas diferem em fase por π / 2 , e cad
Duas fontes sonoras oscilam em fase com uma frequência de 100H z . Em um ponto a 5,00m de uma das fontes e a 5,85m da outro, a amplitude do som proveniente da cada fonte, em separado, é A . (a) Qual é