Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.6 - Ex. 35
Duas ondas senoidais de mesma frequência se propagam no mesmo sentido em uma corda. Se , , e , qual é a amplitude da onda resultante?
Passo 1
Show de bolinhas galerinha, o exercício nos diz que duas ondas senoidais de mesma frequência se propagam no mesmo sentido em uma corda. Sabendo que , , e , o enunciado quer que a gente encontre a amplitude da onda resultante.
Belezoca, temos duas ondas se propagando no mesmo meio com o mesmo sentido: vamos ter interferência.
Aqui a gente tem duas opções para resolver: podemos usar álgebra ou montar um diagrama de fasores.
A segunda é absurdamente mais fácil, e na maioria das vezes é o que as provas querem que a gente faça mesmo, então bora nela.
Então só lembrando: com um diagrama de fasores, a gente vai representar a onda por uma “seta” que gira em um plano cartesiano.
O comprimento da seta é como se fosse a amplitude da onda, e a frequência angular com que ela gira em torno da origem é a frequência angular da onda. Todas as outras propriedades são consequência dessas duas.
Passo 2
Como as duas ondas tem a mesma frequência, vamos imaginar duas setas girando em um plano (em torno da origem) com a mesma velocidade.
Além disso, a diferença de fase entre elas é:
Ou seja, a situação inicial é essa:
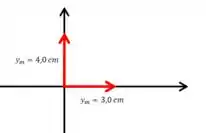
Com os ângulos encostados nos eixos pra ficar mais fácil, o importante é ter a diferença de entre eles.
Passo 3
A grande vantagem dos fasores é que podemos fazer operações entre eles como se fossem vetores.
A onda que resulta da “soma” dessas duas, por exemplo, é representada pela soma vetorial desses dois que foram desenhados.
E então a amplitude da onda resultante é o comprimento do fasor resultante.
Usando o teorema de Pitágoras:
Resolvido!
Resposta
A amplitude resultante é