Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 9ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 9º - Capítulo 22.Problemas Adicionais - Ex. 78
Duas partículas com a mesma carga positiva q são mantidas fixas no eixo y, uma em y =d e a outra em y = - d. (a) Escreva uma expressão para o módulo E do campo elétrico em pontos do eixo x dados por x = αd. (b) Plote E em função de a no intervalo O
Passo 1
a) duas partículas colocadas em pontos simétricos no eixo y (y=d e y=-d) geram um campo no eixo x que só tem componente x, pois as componentes em y são simétrica e de sentido contrário, se anulando assim. Para um ponto qualquer no eixo x podemos construir a seguinte imagem:
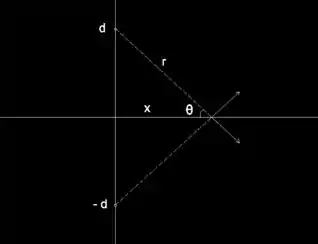
A componente x do campo será:
Usando Pitágoras conseguimos reescrever r em função de x:
o cosseno também pode ser escrito em função de x:
Sendo assim a equação do campo fica:
Para valores de x múltiplos de d temos:
Passo 2
b) Plotando o gráfico para a constante multiplicativa igual a 1 temos:
O gráfico fica:
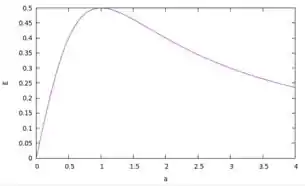
Passo 3
c) Para encontrar o ponto de máximo derivamos a expressão do campo, igualamos a zero e resolvemos para x. A expressão da deriva fica:
Que se anula para o valor
Resposta
Ei, a resposta está no passo a passo :)