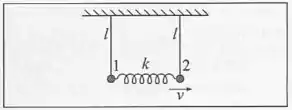
Duas partículas de mesma massa, igual a , estão suspensas do teto por barras idênticas, de de comprimento e massa desprezível, e estão ligadas uma à outra por uma mola de constante elástica . No instante , a partícula recebe um impulso que lhe transmite uma velocidade de . Determine os deslocamentos e das posições de equilíbrio das duas partículas (em ) para

A primeira condição inicial diz que as duas partículas partem do equilíbrio:

Então:

Como as amplitudes , então uma solução possível é:

E como , nós podemos reescrever nossa equação como:

E agora, para aplicar a segunda condição inicial, precisamos tirar as duas derivadas:

E as condições iniciais são:

Então ficamos com um sistema:

Somando as duas temos:

E subtraindo a segunda da primeira:

Então as nossas equações são:

Agora falta calcular e . As fórmulas para essas frequências também são dadas no livro.

é a frequência natural de oscilação do pêndulo, dada por:

E a frequência é:

Onde :

Vamos substituir isso nas nossas equações:

Então: