Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 4.Problemas - Ex. 15
Duas partíclas de mesma massa deslocam-se com atrito desprezível sobre uma superfície horizontal, pesas por molas de constante elástica a paredes verticais e ligadas uma à outra por uma mola de constante elástica . Inicialmente, com as partículas em repouso na posição de equilíbrio, comunica-se uma velocidade à particula através de um impulso. Ache os deslocamentos e das duas partículas das respectivas posições de equilíbrio, para .
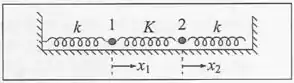
Passo 1
Vamos montar uma EDO para cada um dos corpos e .
Para o primeiro corpo:
E o termo aparece no segundo termo porque a “contração” da mola não depende só de , e sim da aproximação ou afastamento dos dois pontos.
E para o segundo corpo:
Então ficamos com um sistema de duas EDOs:
E definindo :
Passo 2
Agora vamos somar as duas equações:
E aqui é comum definir uma variável:
E fazendo a diferença das duas EDOs do sistema (a segunda menos a primeira):
E mais uma vez vamos definir uma variável:
Vamos chamar esse último termo entre parênteses de . Então ficamos com duas equações:
E as duas soluções são:
Passo 3
Agora vamos voltar para as coordenadas e :
E aplicando a condição inicial :
E podemos usar a solução . Lembrando que :
E agora vamos aplicar e :
E somando as duas equações encontramos:
E então:
Onde e .
Resposta
Os deslocamentos são e , com e .