Duas partículas oscilam em movimento harmônico simples ao longo de um segmento retilíneo comum de comprimento . As duas partículas têm um período de , mas existe uma diferença de fase entre seus movimentos. (a) Qual é a distância entre as partículas (em termos de ) após a partícula atrasada passar por uma das extremidades da trajetória? (b) Nesse instante, as partículas estão se movendo no mesmo sentido, em sentidos opostos se aproximando uma da outra ou em sentidos opostos se afastando uma da outra?
Passo 1
A questão não é muito específica, mas a gente pode pensar, por exemplo, em duas bolinhas presas em molas, que entram em movimento harmônico simples de período quando você dá um peteleco nelas.
Só que imagine que você deu o segundo peteleco alguns instantes depois do outro, de forma que essa era a situação no momento em que começou o movimento da segunda bolinha:
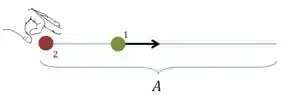
(Imagine as bolinhas presas em molas!) Esse atraso da bola 2 se traduz na diferença de fase de .
Vamos tentar escrever as funções de cada bola nessa forma aqui:
Passo 2
A questão já dá alguns dos parâmetros dessa função. Por exemplo, se o período é , dá pra deduzir que:
Além disso, se o “comprimento total” do movimento é , então a amplitude do movimento é metade disso:
Ou seja:
Agora é só ajustar as constantes de fase, pra representar o atraso da bola .
Passo 3
A letra (a) quer saber qual vai ser a distância entre as duas bolas depois de a partícula atrasada passar por uma das extremidades.
A nossa fórmula já foi feita pra essa situação: é só dar uma olhada na nossa figura lá em cima, o tempo é justamente quando a partícula atrasada está saindo de uma extremidade.
Então agora é só calcular as duas posições no tempo
Beleza, agora a distância entre eles vai ser:
E essa é a resposta da letra (a).
Passo 4
A letra (b) quer saber os sentidos em que as partículas estão viajando nesse momento
Bom, pra isso vamos precisar achar as funções que dão a velocidade das bolas. Pra fazer isso é só derivar a função da posição em relação ao tempo:
E:
Agora é só calcular os valores dessas funções quanto .
Como as duas velocidades tem o mesmo sinal, as duas bolas estão se movendo no mesmo sentido.
Resolvido!
Resposta
(a)
(b) Se movendo no mesmo sentido.