Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.2 - Ex. 34
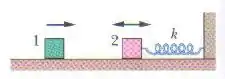
Na figura, o bloco , de massa , oscila na extremidade de uma mola em MHS com um período de . A posição do bloco é dada por . O bloco , de massa , desliza em direção ao bloco com uma velocidade de módulo , dirigida ao longo do comprimento da mola. Os dois blocos sofrem uma colisão perfeitamente inelástica no instante . (A duração da colisão é muito menor que o período do movimento.) Qual é a amplitude do MHS após a colisão?
Passo 1
Belezera galerinha, agora a situação fica um pouco mais complicada, porque o bloco está em movimento no instante da colisão.
Mas calma lá meu patrão, vamos usar a função que o enunciado deu pra achar a posição do bloco no instante da colisão, tal que:
Pra podermos usar essa função, precisamos achar o valor de , mas como já temos o período , podemos fazero seguinte:
Tal que:
Convertendo tudo para metros e segundos, obtemos que:
Logo:
Ou seja, no momento da colisão, o bloco está no extremo negativo do comprimento, onde a mola está totalmente comprimida.
A questão deu o valor da amplitude, de forma que:
Passo 2
Belezera, agora que temos essa informação, vamos calcular a velocidade do sistema após o choque.
Como a colisão é perfeitamente inelástica, sabemos que os dois blocos permanecem juntos depois da colisão. Então a lei de conservação do momento linear fica assim:
A gente acabou de ver que, no momento da colisão, o bloco está comprimindo ao máximo a mola, ou seja, a velocidade é nula.
Substituindo os outros valores, achamos o seguinte:
Passo 3
Show de bolinhas, agora temos todas as informações pra calcular a energia total do sistema depois da colisão.
Como a velocidade depois da colisão é , a energia cinética vai ser:
Logo:
E como a mola está comprimida em , a energia potencial vai ser:
O único problema é calcular a constante elástica , mas vamos deixar ele aí por enquanto, e no final calculamos. A energia total fica então:
Passo 4
Agora que temos a energia total do novo movimento, podemos calcular a amplitude dele usando aquela fórmula de sempre:
Onde é a amplitude do novo movimento, dessa forma obtemos que:
Isolando , vemos que:
Passo 5
Agora podemos calcular o valor de a partir da frequência angular :
Onde:
Obs.: Usamos só a massa porque essa frequência é do movimento do bloco antes da colisão. Sendo assim:
Agora sim, substituindo esse valor na fórmula de cima, veremos que:
Portanto:
Resposta
A amplitude será .