Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 3.Problemas - Ex. 30
A distância entre as cidades e é . Um avião faz uma viagem de ida e volta entre e , voando em linha reta, com velocidade em relação ao ar. (a) Calcule o tempo total de voo, se o vento sopra com velocidade , numa direção que forma um ângulo com a direção . Este tempo depende do sentido em que o vento sopra? (b) Mostre que a viagem de ida e volta só é possível se , e calcule a relação entre o tempo de vôo quando o vento sopra na direção e o tempo , quando sopra na direção perpendicular (este resultado é relevante na discussão da experiencia de Michelson e Morley); (c) Mosstre que, qualquer que seja sua direção, o vento sempre prolonga a duração da viagem de ida e volta.
Passo 1
O que a gente vai ter que reparar aqui é que o avião não pode viajar com sua velocidade em relação ao ar em direção a , porque o vento, apontando em direção diferente dessa, fará com que a soma vetorial das velocidades não permita que o avião chegue no destino.
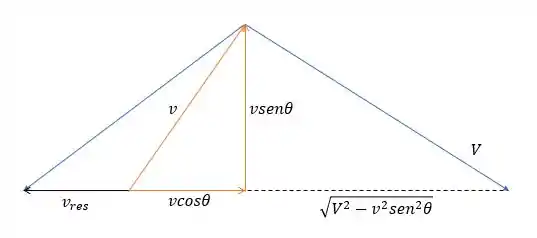
A velocidade resultante vai depender do lado para onde a velocidade do avião aponta. Na ida, está a favor do movimento, mas na volta está contra! Então os tempos vão ser:
Então o tempo total é:
Fazendo o mmc:
Da relação fundamental:
Passo 2
Quando o vento é paralelo, ou .
Quando o vento é perpendicular, ou .
Daqui a gente sabe que:
A razão é:
Passo 3
Queremos provar que essa fração é maior que , ou seja, .
Agora pensa! O vai diminuir no máximo daquele , então o lado esquerdo é maior ou igual a . Enquanto isso, o lado direito é uma fração menor que , já que . Então, o lado esquerdo é sempre maior que o direito, e está provado!