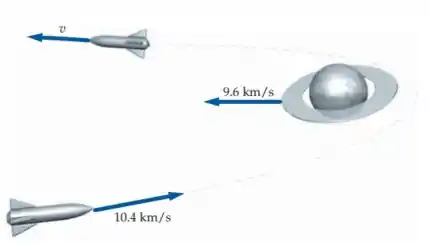
No efeito estilingue, a transferência de energia em uma colisão elástica é usada para dar energia a uma sonda espacial, para que ela possa escapar do sistema solar. Todos os valores de rapidez são em relação a um referencial inercial no qual o centro do Sol permanece em repouso. A figura mostra uma sonda espacial se movendo a de encontro a Saturno, que se move a de encontro à sonda. Devido à atração gravitacional entre Saturno e a sonda, esta contorna Saturno e passa a se orientar no sentido oposto, com rapidez . (a) Supondo esta colisão como unidimensional e elástica, e a massa de Saturno sendo muito maior do que a da sonda, determine . (b) De que fator a energia cinética da sonda aumenta? De onde vem esta energia?

Depois que a gente acha , a gente precisa achar nossas velocidades relativas ao centro de massa do sistema sonda+Saturno (já que essas velocidades que a gente tem são em relação ao Sol).

E como faz isso? Cara, a gente pega a velocidade do objeto e subtrai a velocidade do centro de massa. Para o planeta vai fica:

E para a sonda:

Essas são as velocidades relativas antes do encontro.

Para achar as velocidades relativas depois do encontro, a gente precisa primeiro inverter o sinal das velocidades que a gente achou:

E para a sonda:

E para achar a velocidade da sonda depois do encontro, mas em relação ao sol novamente, a gente pega a velocidade relativa depois do encontro e soma com a velocidade do centro de massa. Assim:

Então a rapidez (módulo da velocidade) da sonda depois desse encontro vai ser igual a .

b) Para achar o fator de aumento da energia cinética a gente divide a energia cinética final (onde ela tem rapidez ) da sonda pela energia cinética inicial (onde ela tem rapidez :

Essa energia vem de uma perda de energia cinética de Saturno (extremamente pequena para ele), que torna-se energia cinética para a sonda.