Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 87
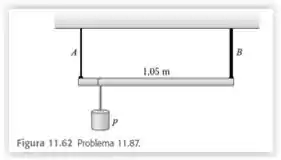
Um eixo de 1,05 m de comprimento e peso desprezível é suportado em suas extremidades por fios A e B de comprimentos iguais (Figura 11.62). A área da seção reta de A é igual a 2,0 e a de B é igual a 4,0 . O módulo de Young de A é igual a ; o de B é igual a . Para qual ponto ao longo do eixo deve o peso p ser suspenso para produzir
a) tensões iguais em A e em B?
b) deformações iguais em A e em B?
Passo 1
E aí, tudo certinho?
Nesse problema temos um eixo de de comprimento e peso desprezível que é suportado em suas extremidades por fios e de comprimentos iguais. A área da seção reta de é igual a e a de é igual a .
O módulo de Young de é igual a ; o de é igual a .
A partir daí queremos saber para qual ponto ao longo do eixo deve o peso ser suspenso para produzir tensões iguais em A e em B e deformações iguais em A e em B.
Tem ideia de como fazemos isso?
Vamos criar um ponto C a uma distância , assim:
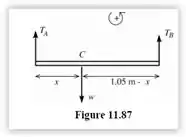
A partir desse ponto podemos aplicar a segunda e a terceira lei de Newton para obter nossos resultados...
Veja só!
Passo 2
Dessa forma, o torque em será zero. E para b,
Como a tensão é igual a , então
Logo,
Tranquilo até aqui?
Passo 3
As deformações podemos encontrar por
Substituindo
Então,
E aí! entendeu tudo? Responde Aí!
Resposta
a)
b)