A figura mostra um inseto capturado no ponto médio do fio de uma teia de aranha. O fio se rompe ao ser submetido a uma tensão de e a deformação correspondente é . Inicialmente, o fio estava na horizontal e tinha um comprimento de e uma área da seção reta de . Quando o fio cedeu ao peso do inseto, o volume permaneceu constante. Se o peso do inseto coloca o fio na iminência de se romper, qual é a
massa do inseto? (Uma teia de aranha é construída para se romper se um inseto otencialmente perigoso, como uma abelha, fica preso na teia.)
Passo 1
Fala povo bacana, bora fazer mais uma?
A gente precisa encontrar a massa do inseto, é interessante pra isso fazer um diagrama de corpo livre do fio, pra gente observar o que acontece.
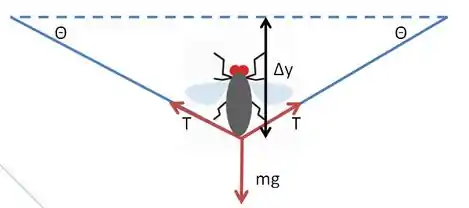
Do equilíbrio vertical do inseto, temos que
tal que é a massa do inseto e a tensão no fio. Lembrando que :
Perceba que se tivermos o valor de e de conseguimos encontrar a resposta pedida (massa do inseto). Vamos encontrá-lo raciocinando por partes nos passos seguintes.
Passo 2
Agora,para encontrarmos , vamos nos concentrar no que acontece com o comprimento do fio após a deformação dele. Observando a figura a gente pode encontrar o valor e fazer uma nova relação.
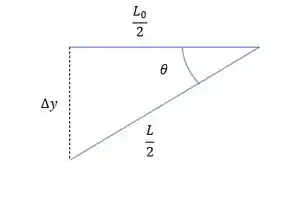
Com o teorema de Pitágoras a gente encontra o
E aí:
Segundo o enunciado, no momento do rompimento, a deformação equivale a , ou seja:
Então, nesse caso, o comprimento do fio após seu esticamento é dado por:
Substituindo esse valor no seno, a gente vai enfim encontrar a relação.
Passo 3
Agora que encontramos uma relação com o ângulo, vamos encontrar a força T e chegaremos a massa do inseto.
Como o volume do fio permanece o mesmo após essa deformação, temos que . Então,
E a tensão no fio é dada por:
E a força isolada é dada por:
Passo 4
Lembrando que a massa do inseto é dada por:
Pois são dois lados do fio, e no caso duas componentes verticais, temos:
Substituindo os valores:
E o valor de seno encontrado, temos: