Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 27.Exercícios e Problemas - Ex. 23

Um elétron é solto, em repouso, a 2,0 cm de um plano infinito carregado. Ele acelera em direção ao plano e colide com ele a uma velocidade de 1,0 ×   10 7 m s . Quais são

  1. a densidade superficial de carga do plano e
  2. o tempo necessário para o elétron percorrer os 2,0 cm?

Passo 1

Faaaaaala, galera... Tranquileba??

Primeiro precisamos saber o campo elétrico perto de um plano de raio infinito.

Assim:

Precisamos definir o campo elétrico do disco a um ponto com uma distancia z do disco. Assim:

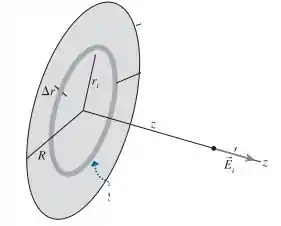
Sabemos pela definição de campo que:

E i = 1 4 π ε 0 ∫ d q r ' 2

Vemos que o campo em x e y se cancelam, logo:

E → = E z cos ⁡ θ = 1 4 π ε 0 ∫ d q r ' 2 cos ⁡ θ

Sabemos que a densidade de carga é dada por:

η = q A

d q = η   d A = η d π r 2 = η 2 π r   d r

Assim:

E → =   1 4 π ε 0 ∫ η 2 π r d r r ' 2 cos ⁡ θ

Para:

r ' = r 2 + z 2 1 2

E:

cos ⁡ θ = r r ' = r r 2 + z 2 1 2

Assim ficando:

E → = E z cos ⁡ θ = 1 4 π ε 0 ∫ η   2 π r d r r 2 + z 2   z r 2 + z 2 1 2 = η z 2   ε 0 ∫ r r 2 + z 2 3 2   d r

Integrando de 0 ≤ r ≤ R , temos que o campo sobre um disco é:

E → = η 2 ε 0 1 - z R 2 + z 2

Para R ≫ z

E = η 2   ε 0

Pede-se η :

η = E * 2   ε 0

Lembrando que:

E = F q

Portanto:

η = F q 2   ε 0

Usando que:

F = m * a

η = m * a q 2   ε 0

Sendo m a massa do eletrone foi nos dado que q = e .

Passo 2

Assim, temos como desconhecido a aceleração. Mas é nos dado a velocidade inicial e final, e a distancia percorrida do elétrons, dessa forma podemos usra a equação de Torricelli:

V f 2 = V 0 2 + 2 * a * Δ S → a = V f 2 - V o 2 2 Δ S

Aplicando os valores:

a = 1 × 10 7 m s 2 - 0 2 * 0.02   m = 2.5 × 10 15 m s 2

Portanto:

η = m * a q 2   ε 0 = 9.11 × 10 - 31   k g * 2 . 5 × 10 15 m s 2 1.6 × 10 - 19 C 2 * 8.85 × 10 - 12 C 2 N m 2

Portanto:

η = 2.5 × 10 - 7 C m 2

Passo 3

Para b)

Sabendo que:

Δ v = a * t → t = Δ v a

Aplicando valoresa:

t = 1 ×   10 7 m s 2.5 × 10 15 m s 2 = 4.0 × 10 - 9   s

Resposta

Para a)

η = 2.5 × 10 - 7 C m 2

Para b)

t = 4.0 × 10 - 9   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um anel de raio a tem uma distribuição de cargas que varia como λ θ = λ 0 sen ⁡ θ , como mostra a figura 22-39. (a) Quais são a direção e o sentido do campo elétrico no centro do anel? (b) Qual é a ma
Uma fina casca hemisférica de raio R tem uma densidade superficial uniforme de carga σ . Determine o campo elétrico no centro da base da casca hemisférica.
Um disco não-condutor de raio R está no plano z = 0 com seu centro na origem. O disco tem uma densidade σ . Determine o valor de z para o qual E z = σ / ( 4 ε 0 ) . Observe que, nesta distância, a int
Mostre que a intensidade do campo elétrico E no eixo de um anel carregado de raio a tem valor máximo em z = ± a / 2 . (b) Esboce a intensidade E do campo versus z para valores positivos e negativos de
Um anel com raio a está no plano z = 0 com seu centro na origem. O anel está uniformemente carregado e tem uma carga total Q . Determine E z no eixo z em (a) z = 0,2 a , (b) z = 0,5 a , (c) z = 0,7 a