Um engenheiro possui um objeto de de forma irregular e precisa conhecer o momento de inércia do objeto em relação a um eixo que passa pelo centro de massa. O objeto é preso a um fio esticado cuja orientação é a mesma do eixo. O fio possui uma constante de torção . Se esse pêndulo de torção sofre oscilações completas em , qual é o momento de inércia do objeto?

Bom galera, essa questão é um pouquinho diferente do que a gente tem visto e isso se dá por que aqui estamos trabalhando com um pêndulo diferente que é o pêndulo de torção.

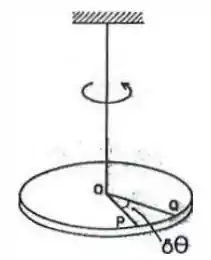
Esse pêndulo ele é diferente pois a oscilação dele vai se dar pelo fato dele rotacionar ao redor do eixo.

Esse eixo é feito de um fio e esse fio tem uma constante de torção (que também é algo novo pra a gente né).

Essa constante de torção vêm da Lei de Hooke para o caso angular (isso é, para rotações).

O mais importante aqui é saber que o torque gerado pelo fio vai ser dado como:

Aonde o é a constante de torção dada e é a posição angular do nosso objeto.

Pela segunda lei de newton para rotações, teremos:

Sendo que a aceleração angular, pode ser reescrita como sendo a segunda derivada da posição angular.

E se juntarmos tudo teremos uma equação diferencial:

Isolando a derivada, temos:

Agora que vem a parte mais importante, essa equação diferencial tem uma resposta que é:

Aonde a frequência angular é:

Opa, apareceu o momento de inércia em termos da frequência angular, agora tá fácil resolver.