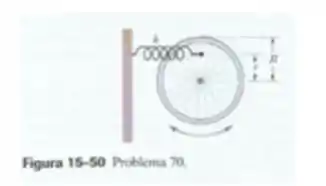
Uma roda pode girar livremente em torno do eixo, que é mantido fixo. Uma mola está presa a um dos raios a uma distância do eixo, como mostra a Fig. 15-50. (a) Supondo que a roda é um anel de massa e raio , qual é a frequência angular para pequenas oscilações deste sistema em termos de , , e da constante elástica ? Qual é o valor de para (b) e (c) ?

Antes, da gente calcular a frequência natural do sistema, vamos calcular a sua energia mecânica total. Sabendo que o momento de inércia da roda é dada por , a energia do sistema fica

Se, agora, a gente transformar a velocidade angular da roda em velocidade linear da mola no ponto de fixação com a roda, e depois substituir na equação da energia, a gente tem que

Substituindo agora na equação da energia

Essa equação se parece com a energia do oscilador harmônico simples. Se nós identificarmos a massa no termo da energia cinética com o termo que aparece neste problema, a gente consegue descobrir a frequência natural de oscilação desse sistema.