Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.Problemas - Ex. 70

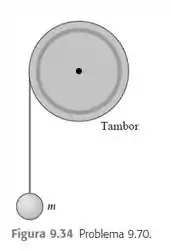
Engenheiros projetam um sistema por meio do qual uma massa m em queda livre imprime energia cinética a um tambor uniforme em rotação, ao qual a massa está presa por um cabo delgado e leve, enrolado em volta do tambor (Figura 9.34). Não há nenhum atrito significativo no eixo do tambor e tudo parte do repouso. Esse sistema está sendo testado na Terra, mas é para ser usado em Marte, onde a aceleração da gravidade é 3,71   m / s 2 . Nos testes na Terra, quando m possui 15,0   k g e deve cair por 5,0   m , ela fornece 250,0   J de energia cinética ao tambor. a) Quando o sistema for operado em Marte, qual distância a massa de 15,0   k g terá que cair para gerar o mesmo valor de energia cinética para o tambor? b) Qual a velocidade da massa de 15,0   k g em Marte quando o tambor obtiver 250,0   J de energia cinética?

Passo 1

Oi, galerinha! Tudo bom?

Repara que nessa questão temos um corpo em queda livre mas preso a um fio que vai girar o tambor, ou seja, está havendo uma transferência de energia.

Deste modo, o que temos que fazer é aplicar a conservação de energia ao sistema t a m b o r + m a s s a   e m   q u e d a e depois comparar os resultados para Terra e para Marte.

Lembrando que a energia cinética do tambor é dada por:

K t a m b o r = 1 2 I ω 2

E a energia cinética da massa pendurada é dada por:

K m a s s a = 1 2 m v 2

Além disso, temos que

v = R ω

então, se K t a m b o r é o mesmo. Temos que ω é o mesmo e v é o mesmo em ambos os planetas. Sendo assim, K m a s s a é a mesma.

Tomando como y = 0 na altura inicial da massa e + y para cima.

Vamos dividir a situação em duas configurações:

1 : q u a n d o   a   m a s s a   e s t á   e m   s u a   p o s i ç ã o   i n i c i a l . 2 : é   q u a n d o   a   m a s s a   d e s c e   5 m

Então,

y 1 = 0

E

y 2 = - h

onde h é a altura em que a massa desce.

Bora lá!

Passo 2

  1. Pela conservação de energia, temos que:

    2. K 1 + U 1 = K 2 + U 2

    Nós só temos energia potencial quando está elevado do chão, ou seja, na nossa situação 2 .

    Assim temos que: U 1 = 0 U 2 = - m g h .

    Portanto, ficamos com:

    0 = K t a m b o r + K m a s s a - m g h

    Mas K t a m b o r + K m a s s a são iguais nos dois planetas, então ficamos só com a parte m g h .

    Como isso, fazemos,

    m g T e r r a h T e r r a = m g M a r t e h M a r t e

    Isso implica em:

    h M a r t e = h T e r r a g M a r t e g M a r t e

    h M a r t e = 5 m ⋅ 9,8 m s 2 3,71 m s 2

    h M a r t e = 13,2 m

    Tranquilo até aqui?

    Passo 3

  2. Para sabermos a velocidade da massa em marte, fazemos a seguinte relação:

m g M a r t e h M a r t e = K t a m b o r + K m a s s a

∴

1 2 m v 2 = m g M a r t e h M a r t e - K t a m b o r

Isso implica em:

v = 2 g M a r t e h M a r t e - 2 K t a m b o r m

v = 2 ⋅ 3,71 m s 2 ⋅ 13,2 m - 2 ⋅ 250 J 15 k g

v = 8,04 m / s

Note que, fizemos os cálculos sem saber o momento de inércia I do tambor, ou a massa e o raio do tambor.

E fim! O que achou? Responde Aí!

Resposta

  1. h M a r t e = 13,2 m
  2. v = 8,04 m / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Como estagiário de uma empresa de engenharia, você é solicitado a medir o momento de inércia de uma grande roda, para girar em torno de um eixo que passa pelo seu centro. Você mede o diâmetro da roda,
A enguia possui uma certa quantidade de energia cinética de rotação ao fazer 14 giros por segundo. Se, em vez disso, ela nadasse em linha reta, com que velocidade ela teria de nadar para ter a mesma q
Você está reformando um Chevrolet 1965. Para decidir se irá substituir o volante por um mais novo e mais leve, você deseja determinar o momento de inércia do volante original, com diâmetro de 35,6 cm.
Você está testando um pequeno volante (raio de 0,166 m) que será usado para armazenar uma pequena quantidade de energia. O volante é pivotado com rolamentos de baixo atrito em torno de um eixo passand
Um disco composto de diâmetro externo de 140,0c m é constituído de um disco maciço uniforme com raio de 50,0c m e densidade de área de 3,0g / c m 2 , cercado por um anel concêntrico com raio interno d