Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 52
Sua equipe é encarregada de lançar um grande balão meteorológico de hélio esférico em forma e cujo raio é de 2,5 me massa total é de 15 kg (balão mais hélio mais equipamentos).
a) Qual é a aceleração inicial ascendente do balão quando é liberado do nível do mar?)
b)Se a força de arrasto no balão é dada por , onde é o raio do balão, é a densidade do ar e a velodicade de ascensão do balão, calcule a velocidade terminal do balão ascendente.
Passo 1
Primeiro vamos imaginar o problema: Temos um balão e queremos achar a aceleração e a velocidade do balão devido as condições iniciais e as formulas de arrasto.
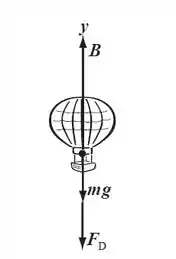
Analisando as forças, temos que: As forças agindo no balão estão a força flutuante B, mg de peso e força de arrasto FD. Nós podemos encontrar a aceleração ascendente inicial do balão aplicando a segunda lei de Newton no instante em que é liberada. Podemos encontrar a velocidade terminal do balão, reconhecendo que quando ay = 0, a força resultante que atua sobre balão será zero. Portanto, temos que:
Passo 2
Usando o princípio de Arquimedes, a gente pode expressar que a força de flutuação no balão é:
Sabendo disso, podemos realocar a nossa equação na equação de cima.
Isolando o nosso , que corresponde a aceleração no eixo y, temos que:
A partir de agora basta substituir os valores numéricos na equação:
Passo 3
Agora temos a aceleração, portanto aplicamos o nosso
Portanto, bastamos inserir os valores numéricos e acahr o valor da velocidade do balão!